FieldsMathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

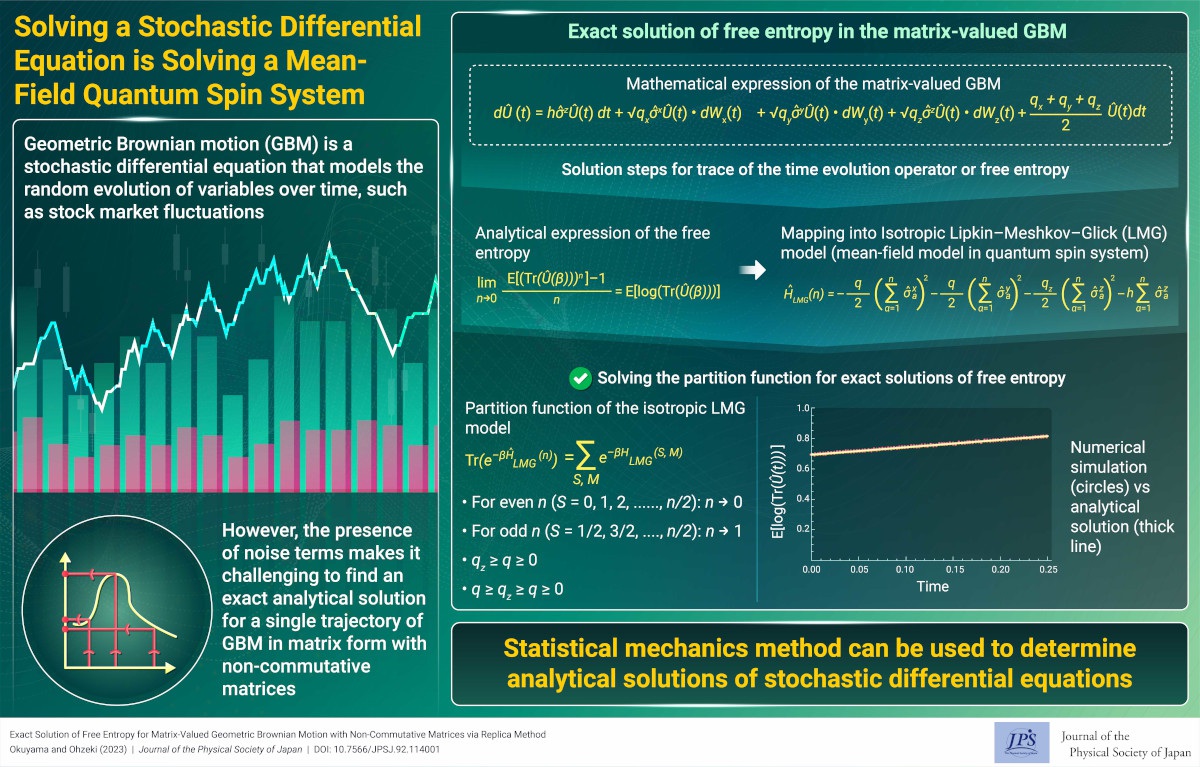
Solving a Stochastic Differential Equation is Solving a Mean-Field Quantum Spin System

The replica method maps matrix-valued geometric Brownian motion to a mean-field quantum spin system. This correspondence makes it possible to obtain an exact solution for matrix-valued geometric Brownian motion.

Statistical physics and thermodynamics

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Magnetic properties in condensed matter

Quantum Mechanics of One-Dimensional Three-Body Contact Interactions

The quantum mechanical description of topologically nontrivial three-body contact interactions in one dimension is not well understood. This study explores the Hamiltonian description of these interactions using the path-integral formalism.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Theoretical Particle Physics

Exploring Recent Advances in the Physics of Biofluid Locomotion

This Special Topics Edition of the JPSJ describes the latest advances in the field of biofluid locomotion, shedding light on the underlying physics behind the movement of organisms that swim and fly.

Measurement, instrumentation, and techniques

Cross-disciplinary physics and related areas of science and technology

Electromagnetism, optics, acoustics, heat transfer, and classical and fluid mechanics

Statistical physics and thermodynamics

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Structure and mechanical and thermal properties in condensed matter

Topological Properties of the Periodic Toda Lattice: Analogy with the Thouless Pump

We find that the periodic Toda lattice belongs to the same topological class as the Thouless pump.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Electronic structure and electrical properties of surfaces and nanostructures

Towards a New Phase in Materials Science with Hyperordered Structures

A Special Topics edition of the Journal of the Physical Society of Japan features articles discussing recent advancements in hyperordered structures in materials, their applications, and the techniques for observing them.

Structure and mechanical and thermal properties in condensed matter

Cross-disciplinary physics and related areas of science and technology

Dielectric, optical, and other properties in condensed matter

Electron states in condensed matter

Atomic and molecular physics

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

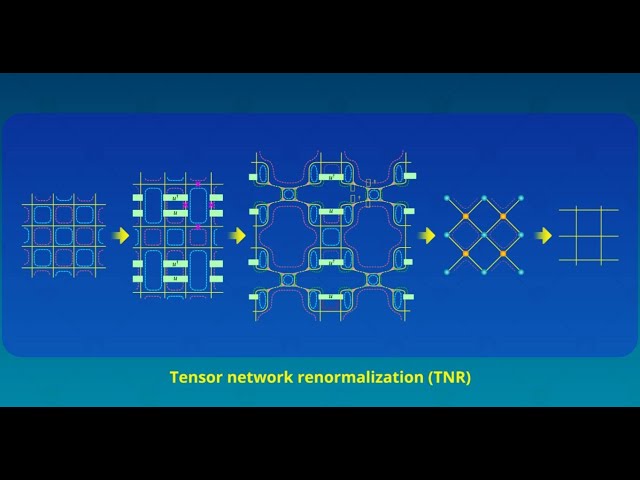
Tensor Networks Across Physics

Researchers from Japan provide the first comprehensive review of the historical development of tensor networks from a statistical mechanics viewpoint, with a focus on its theoretical background.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Statistical physics and thermodynamics

Magnetic properties in condensed matter

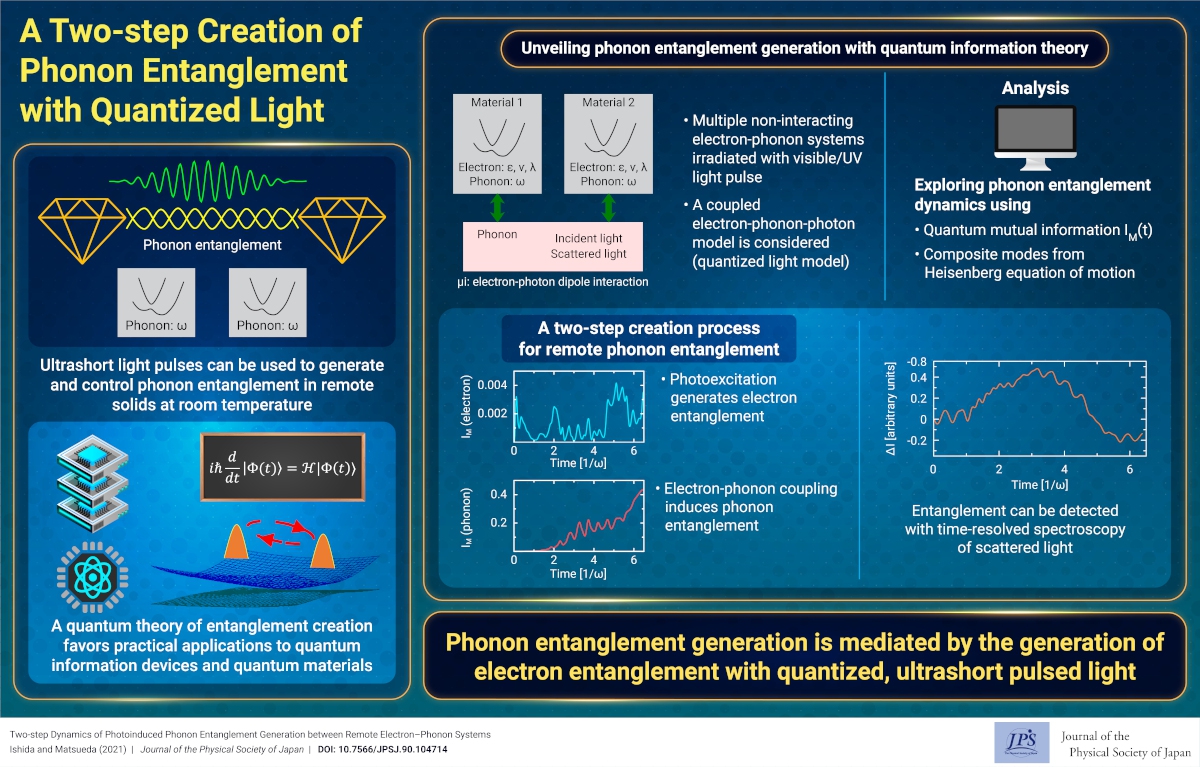
A Two-step Creation of Phonon Entanglement with Quantized Light

Dynamics of photoinduced quantum entanglement generation between phonons is theoretically revealed. The results contribute to the study of fundamental theoretical problems within quantum dynamics of photoinduced phase transitions and quantum information science.

Dielectric, optical, and other properties in condensed matter

Electromagnetism, optics, acoustics, heat transfer, and classical and fluid mechanics

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Generalizing Poisson Algebra with Geometry

Using a differential geometric interpretation of Hamiltonian mechanics, a generalized Poisson bracket formulation is developed for a three-dimensional phase space characterized by a triplet of canonical variables.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Atoms Trapped with Light Behave Like a Dissipative Quantum System

A team of researchers from Japan experimentally realize, for the first time, a dissipative, parity-time symmetric, many-body quantum system from ultracold atoms trapped in an optical lattice.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Gases, plasmas, electric discharges, accelerators, and beams

A Quantum Description of Physical Systems with Non-real Energies

While quantum systems are traditionally described by Hermitian Hamiltonians, the formalism is extendable to a non-Hermitian description for systems that are dissipative or obey parity-time symmetry.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Nuclear physics

Electron states in condensed matter

Gases, plasmas, electric discharges, accelerators, and beams

Random Numbers Can Help Solve Difficult Problems in Many-body Physics

Theorists review a random state vector-based description of quantum many-body systems which helps greatly reduce the computational burden involved in their numerical simulations, opening doors to applications in quantum computing.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Electronic transport in condensed matter

Magnetic properties in condensed matter

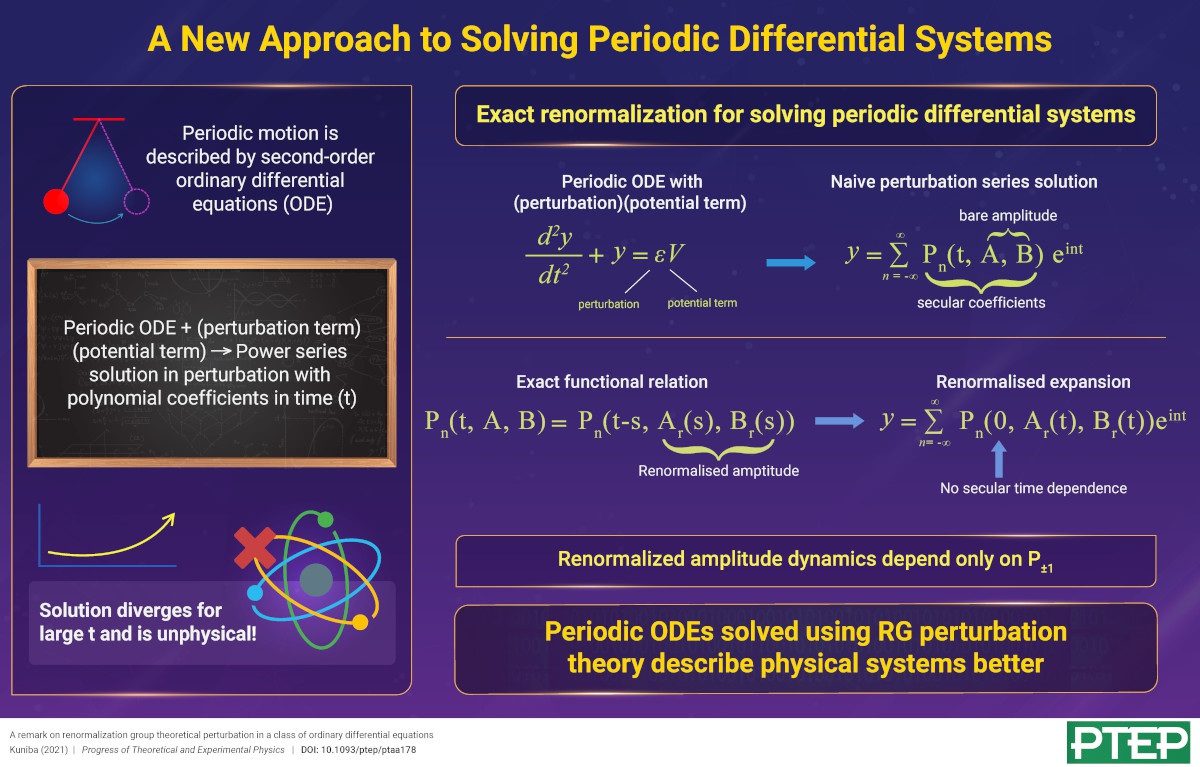
A New Approach to Solving Periodic Differential Systems

Mathematicians and physicists are well acquainted with second-order ordinary differential equations (ODE), the most prominent of them being the class of equations that govern oscillatory motion.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Hybrid Quantum–Classical Algorithms: At the Verge of Useful Quantum Computing

Scientists discuss the recent progress in algorithms that have enabled hybrid quantum–classical computers, which has brought the quest to realize useful quantum computing much closer to its finish line.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Cross-disciplinary physics and related areas of science and technology

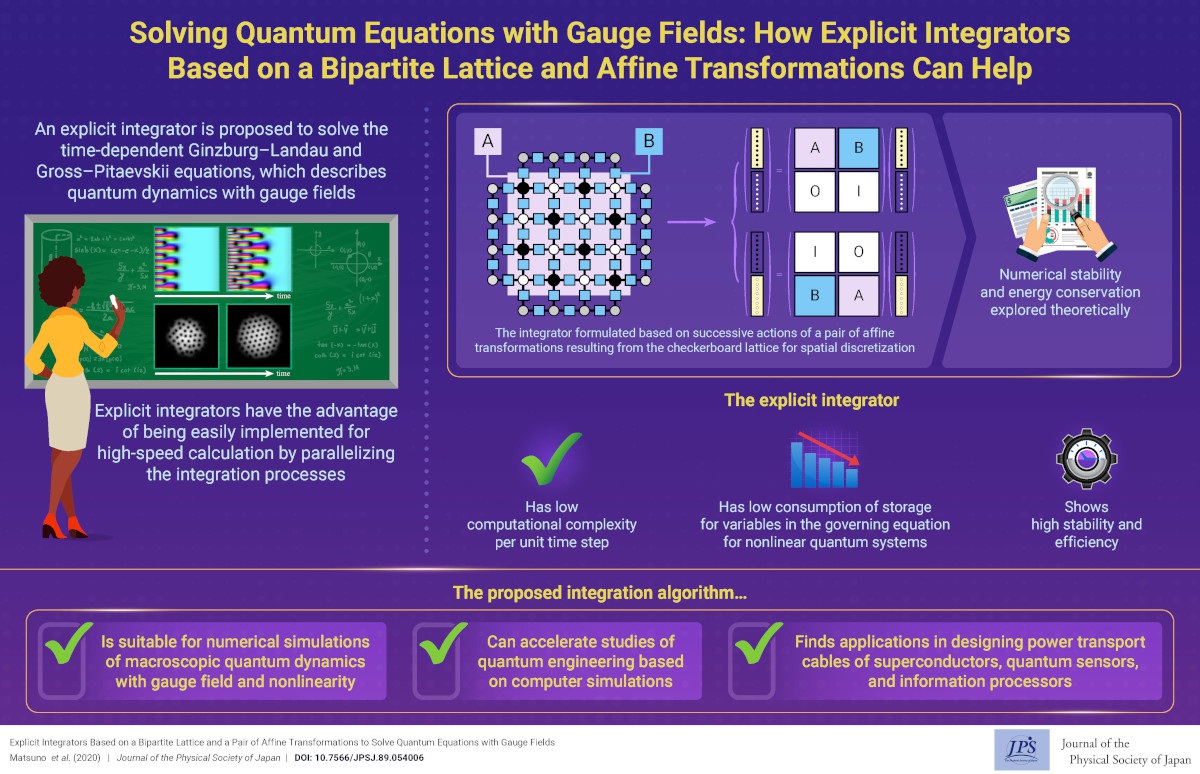
Solving Quantum Equations with Gauge Fields: How Explicit Integrators Based on a Bipartite Lattice and Affine Transformations Can Help

We proposed an explicit numerical integrator consisting of affine transformation pairs resulting from the checkerboard lattice for spatial discretization. It can efficiently solve time evolution equations that describe dynamical quantum phenomena under gauge fields, e.g., generation, motion, interaction of quantum vortices in superconductors or superfluids.

Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling

Superconductivity