A New Approach to Solving Periodic Differential Systems

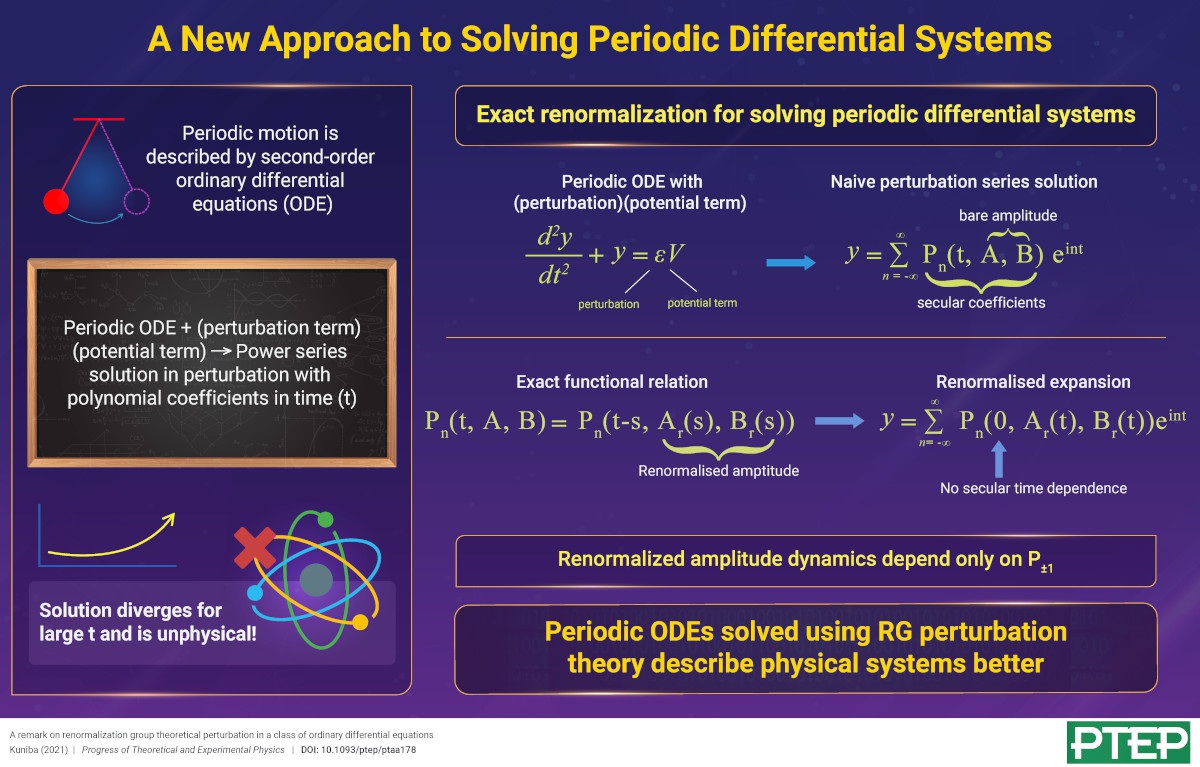
Mathematicians and physicists are well acquainted with second-order ordinary differential equations (ODE), the most prominent of them being the class of equations that govern oscillatory motion. Often, these oscillatory-type equations involve an inhomogeneous “potential” term coupled with a perturbation term and are usually solved as a power series in the perturbation with coefficients that are polynomials in the independent variable. However, when describing time-dependent behavior of a system, i.e., the independent variable is time (t), the series solution becomes problematic due to the coefficients diverging in time, which limits the valid description of the system to time scales of the order of (1/perturbation).

In a new study, I report on an elegant (yet unnoticed) functional identity in renormalization group (RG) theoretical perturbation theory, which is useful to get rid of the divergent time-dependence and to replace it instead with a description based on “renormalized amplitudes” and their time dynamics.

I begin with a second-order ODE in time with a potential term depending on the perturbation, the independent variable and its derivative, and the “resonant harmonics,” e^±it, and its naïve perturbation series solution. Next, I write the dependent variable, say y, as a perturbation series expansion and substitute it in the ODE to get an equation for each power of the perturbation. I define Y as the resulting formal solution of the power series expansion of y and write it as a Fourier expansion with coefficients that are functions of what I call “bare amplitudes,” A, B. I will formally refer to them as “secular coefficients.”

I go on to prove an identity and a relation between the secular coefficients that are key to my results. I next define the “renormalized amplitudes” A_r(t) and B_r(t) as a function of the “resonant” secular coefficient and use the proved relation to express the bare amplitudes as a function of A_r(t) and B_r(t). Using the identity proved before, I further establish the renormalized series expansion in terms of A_r and B_r, which is free from the secular time dependence.

Further, the dynamics of A_r(t) and B_r(t) is solely determined by the resonant secular coefficients to all orders of perturbation.

This work has important implications in studies involving the classic cases of Van der Pol, Mathieu, Duffing, and Rayleigh equations and may trigger new theoretical development of a RG-based approach to solving differential equations.