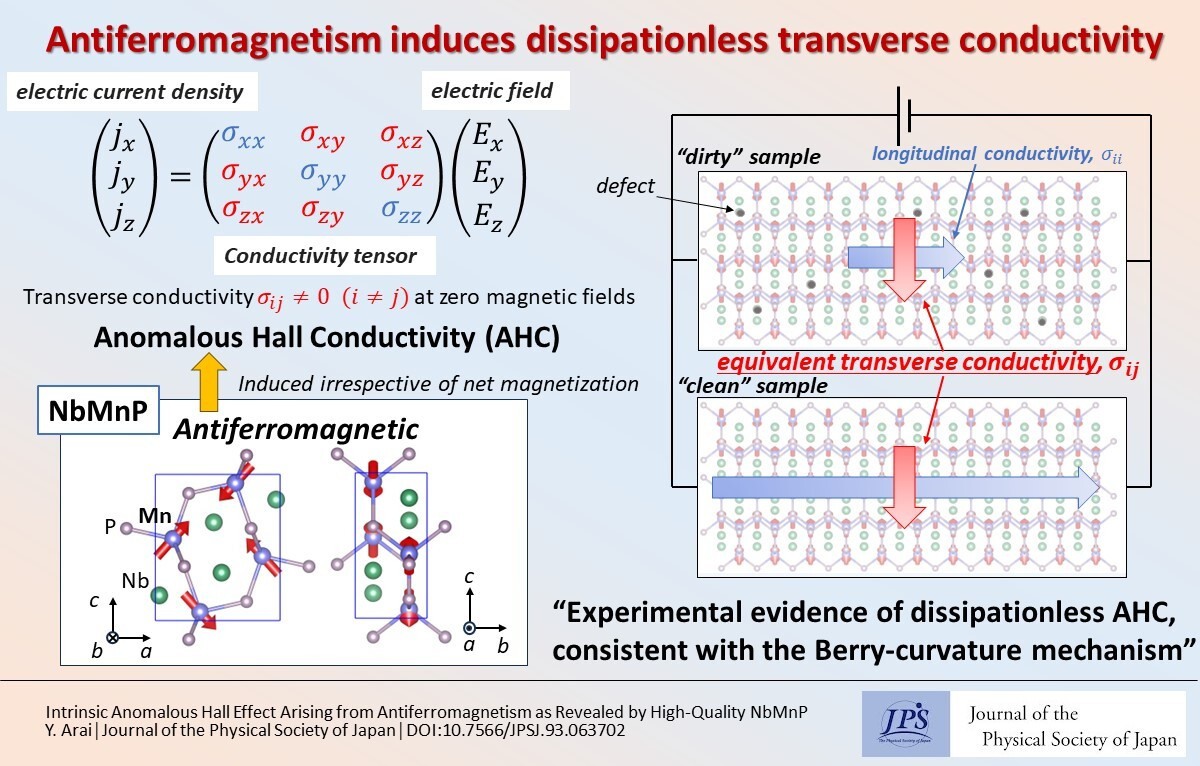
The anomalous Hall effect (AHE) is the Hall effect that emerges at zero magnetic fields. It was discovered in ferromagnets more than 100 years ago; however, its mechanism had long been controversial. In the 2000s, the band-structure effect, known as the intrinsic mechanism, was reconstructed based on the Berry phase concept. Many theoretical and experimental investigations revealed that the intrinsic mechanism contributes significantly to the AHE in ferromagnets. This is experimentally confirmed by observing the scattering dependence of the anomalous Hall conductivity (AHC), i.e., the transverse conductivity, because the intrinsic mechanism contributes to a dissipationless AHC, which is independent of scattering.
Meanwhile, the Berry phase concept clarifies that the AHE is not triggered by magnetization but by symmetry breaking. This resulted in the discovery of the prominent AHEs in antiferromagnetic (AF) materials. Several AF materials exhibiting the AHE have been discovered; however, a system that can offer high-quality crystals has not been discovered. The scattering dependence of the AHC arising from AF structures must be investigated.
In this study, high-quality crystals with large AHE arising from the AF structure were obtained in NbMnP using the Ga-flux method. Using high-quality NbMnP, we investigated the scattering dependence of the AHC against a wide range of electrical conductivities. Consequently, dissipationless AHC was experimentally confirmed for the AF material.
The prospective benefits of obtaining high-quality NbMnP are not limited to understanding the AHE. This AF material is expected to generate other ferromagnetic responses, such as the anomalous Nernst effect (ANE). Influence of disorder on the ANE has not been investigated comprehensively, including that for ferromagnets; thus, their impurity dependence must be elucidated. NbMnP is a suitable material for assessing the effect of impurities on ferromagnetic responses under the AF spin configuration.
(Written by Y. Arai on behalf of all authors.)
]]>