Solving Quantum Equations with Gauge Fields: How Explicit Integrators Based on a Bipartite Lattice and Affine Transformations Can Help
© The Physical Society of Japan
This article is on
Explicit Integrators Based on a Bipartite Lattice and a Pair of Affine Transformations to Solve Quantum Equations with Gauge Fields
(JPSJ Editors' Choice)
J. Phys. Soc. Jpn. 89, 054006 (2020).
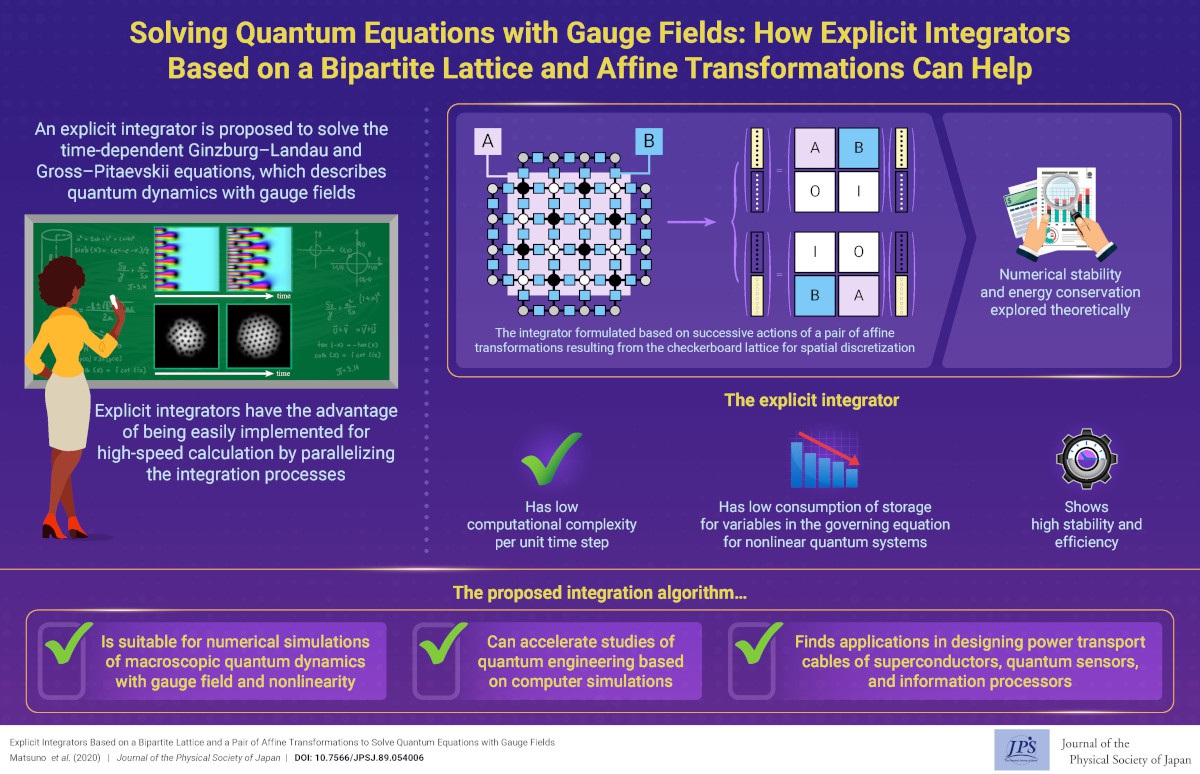
We proposed an explicit numerical integrator consisting of affine transformation pairs resulting from the checkerboard lattice for spatial discretization. It can efficiently solve time evolution equations that describe dynamical quantum phenomena under gauge fields, e.g., generation, motion, interaction of quantum vortices in superconductors or superfluids.
Explicit Integrators Based on a Bipartite Lattice and a Pair of Affine Transformations to Solve Quantum Equations with Gauge Fields
(JPSJ Editors' Choice)
J. Phys. Soc. Jpn. 89, 054006 (2020).
Share this topic
Fields
Related Articles
-
Measurements and Implications of Shot Noise in Mesoscopic Systems
Electronic transport in condensed matter
Magnetic properties in condensed matter
Superconductivity
2021-9-29
Shot noise measurements provide rewarding insights into system properties, non-equilibrium phenomena, and quantum effects in mesoscopic systems.
-
Generalizing Poisson Algebra with Geometry
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
2021-9-6
Using a differential geometric interpretation of Hamiltonian mechanics, a generalized Poisson bracket formulation is developed for a three-dimensional phase space characterized by a triplet of canonical variables.
-
Semiconductor to Semimetal to Superconductor: An Excitonic Journey
Superconductivity
Electronic transport in condensed matter
2021-8-16
A phase diagram was constructed for Ta2NiSe5, a promising candidate for excitonic insulators, using high pressure as a tuning parameter. The results indicated pressure-induced superconductivity in the semimetallic phase.
-
Atoms Trapped with Light Behave Like a Dissipative Quantum System
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Gases, plasmas, electric discharges, and beams
2021-7-19
A team of researchers from Japan experimentally realize, for the first time, a dissipative, parity-time symmetric, many-body quantum system from ultracold atoms trapped in an optical lattice.
-
A Quantum Description of Physical Systems with Non-real Energies
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Nuclear physics
Electron states in condensed matter
Gases, plasmas, electric discharges, and beams
2021-7-19
While quantum systems are traditionally described by Hermitian Hamiltonians, the formalism is extendable to a non-Hermitian description for systems that are dissipative or obey parity-time symmetry.