New Systematic Analysis Method of Identifying Microscopic Essential Couplings

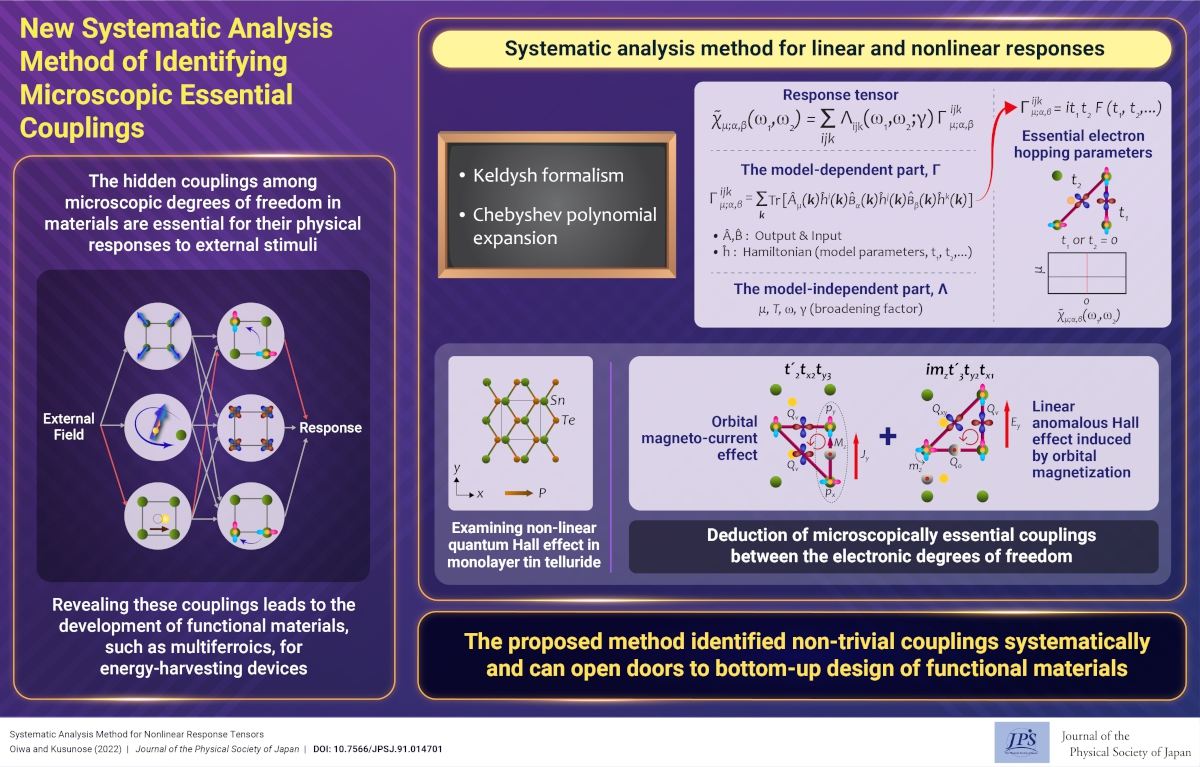
Discovering physical responses and elucidating their microscopic mechanisms are central subjects in condensed matter physics. Recently, various linear and nonlinear responses, such as the anomalous Hall effect under antiferromagnetic orderings and nonlinear optoelectronic transport, have been extensively investigated. These responses have been mainly analyzed theoretically by electronic-structure calculation, group-theoretical argument with electronic multipoles, and Berry curvature interpretation in the context of the topology of electronic states. These approaches have their own advantages: the electronic-structure calculation takes account of the complicated electronic band structures quantitatively, while the argument with the electronic multipoles can identify the relevant electronic degrees of freedom from the symmetry viewpoint.

However, in reality, the system contains numerous model parameters, making it difficult to determine the most important factor in various linear and nonlinear responses. Thus, identifying the essential parameters in the responses is significant to obtain a deeper understanding of multiferroic responses, and once determined, they provide a microscopic picture of the response. In other words, minimal couplings among the model parameters, such as electron hopping and spin-orbit coupling, and electric and/or magnetic order parameters are identified, and they provide a useful guideline for designing novel functional materials.

We proposed a systematic analysis method for linear and nonlinear responses that enables us to extract essential model parameters from a large number of parameters of a given theoretical model. Using the Keldysh formalism and Chebyshev polynomial expansion method, the response tensors are decomposed into model-independent and model-dependent parts; the latter is expressed as a power series of the Hamiltonian matrix and operators describing the external input and resultant response. By analyzing the low-order contributions in the model-dependent part analytically, we can identify essential parameters and deduce a microscopic picture of the response as a minimal coupling between the degrees of freedom associated with the essential parameters. We demonstrated our method by analyzing the nonlinear Hall effect in the ferroelectric SnTe monolayer and elucidated the significance of a second-neighbor diagonal hopping with an orbital exchange that always exists regardless of ferroelectric ordering.

The present method is applicable to a wide range of materials such as inorganic/organic molecules and quantum dots because it is not restricted to the periodicity of the crystal. Similarly, the present systematic analysis method reveals hidden couplings between transfer integrals, spin-orbit coupling, and order parameters in various materials, and is expected to provide a useful design guideline for future functional materials.

(Written by R. Oiwa on behalf of all authors)