A Neural Thermometer for Predicting Phase Transitions of Unknown Systems

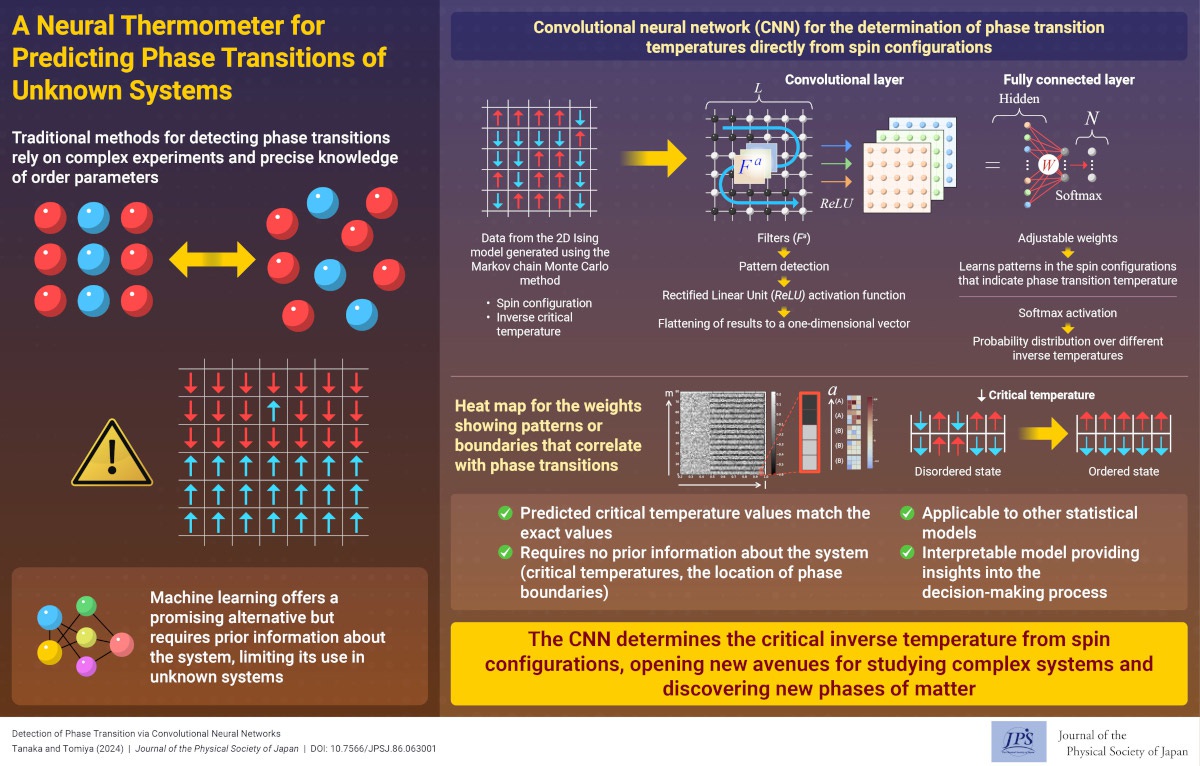
Machine learning has revolutionized research in fields hindered by experimental limitations. One notable application is identifying phases of matter that are classified by order parameters, which measure the degree of order within a system and signal phase transitions. These transitions can range from simple solid-liquid transformations to complex changes in magnetization or superconductivity. Identifying order parameters requires precise measurements that are often challenging with current technology. Additionally, some phases, like topological phases, lack clear order parameters, making them difficult to analyze.

Convolutional neural network (CNN)-based machine learning techniques have successfully classified phases in two- and three-dimensional systems. However, these techniques require labeled data, such as known phases or critical temperatures where phase transitions occur, to identify patterns and train the model. This limitation restricts their use for studying unknown systems, where information is not readily available.

In our study, we developed a novel CNN to determine phase transition temperatures directly from spin configurations of the system. The CNN consists of a convolutional layer that extracts patterns from the spin configurations, a single hidden layer, and a fully connected layer for (inverse) temperature prediction. We trained the CNN on data generated from the 2D Ising model, a simplified model of a magnetic system where spins are aligned either up or down on a 2D grid or lattice. In such a system, the spins tend to align below the critical temperature (the phase transition temperature), resulting in a magnetized phase. Using data generated through Monte Carlo simulations of the Ising model, the weights in the trained neural network captured features of the various spin configurations that signal phase transitions, enabling accurate prediction of critical temperatures.

Our model's predictions of ferromagnetic phase transition temperatures closely matched the exact solutions. Although we used data generated by the Monte Carlo method for training, the model can also be applied to real data. The model is unique in that even though it was trained to just predict the (discretized) inverse temperatures of the inputs, it acquired the notion of phase transition coincidentally. This makes it particularly useful for studying completely unknown systems and statistical models in condensed matter physics. Additionally, unlike many neural networks that operate as black boxes and do not explain their predictions, this model provides insight into how it reaches its decisions in predicting critical temperatures, making it valuable for system analysis. For these contributions, our study received the Outstanding Paper Award from the Physical Society of Japan.