Evaluation of the Exchange Stiffness Constants of Itinerant Magnets from the First-Principles Calculations

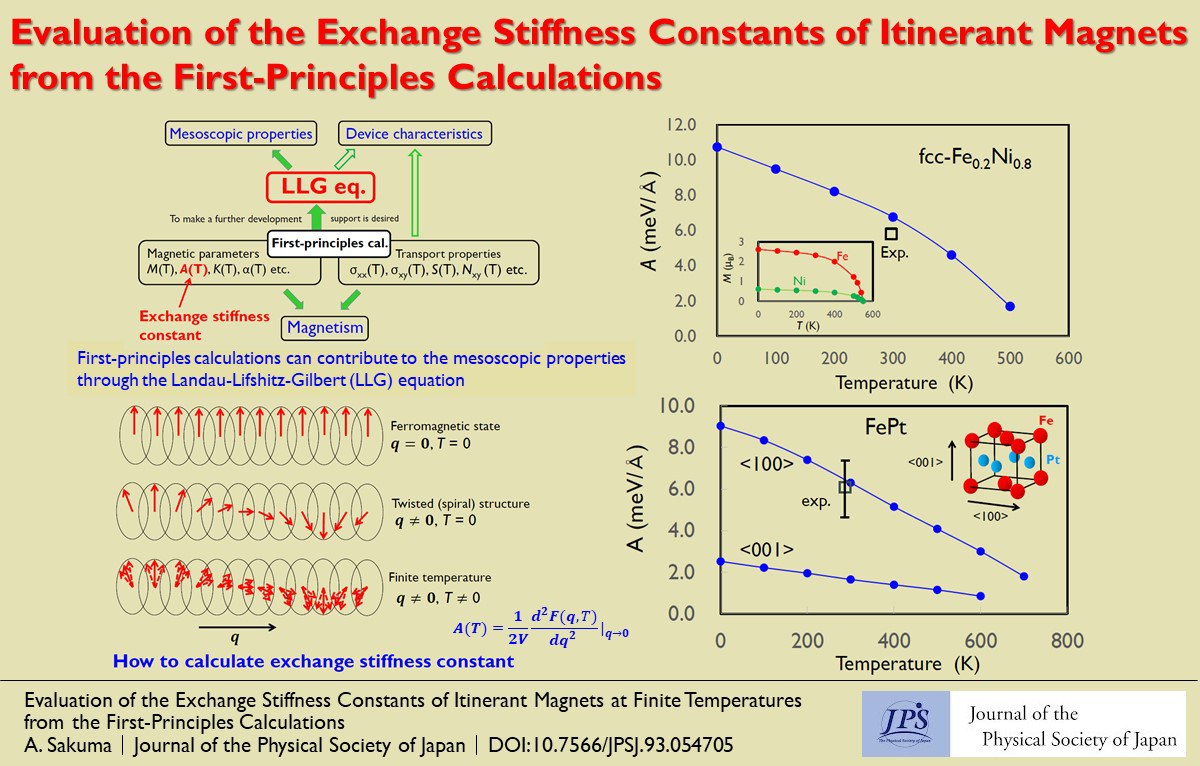
First-principles calculations based on electronic theory are powerful method for quantitatively representing the individuality of materials without the need for adjustable parameters. However, most industrial materials are far from perfect crystals and exhibit many defects such as vacancies, grain boundaries, and strains. Currently, it is difficult to describe the properties of these practical materials solely via first-principles calculations, and coarse graining based on the stiffness or characteristic length of order parameters is required. In such scale regions, the equations, such as the Landau-Lifshitz-Gilbert (LLG) equation for magnetism, are effective. This equation enables visualization of the macroscopic behavior of the order parameters (magnetization) in complex environments. Based on this perspective, the role of the first-principles calculations is to provide the parameters (magnetic constants) constituting the LLG equation.

The magnetic constants that constitute the LLG equation include the exchange stiffness constant (𝐴), magnetic anisotropy constant (K), and Gilbert damping constant (α). The issue arises because the interest in material properties predominantly focuses on room temperature or higher temperature regimes. Hence, the challenge involves determining the magnetic constants at finite temperatures from a microscopic standpoint. With respect to general metallic ferromagnets, functional integral methods have been powerful prescriptions for the finite temperature magnetism.

In this study, we focus on the first-principles calculations of the exchange stiffness constant 𝐴 at finite temperatures based on the functional integral method. The exchange stiffness constant is a measure of the rigidity (or hardness) of regular spin arrangements (such as ferromagnetic alignments) arising from the exchange interaction between spins. To evaluate 𝐴(𝑇), a spiral magnetic structure characterized by wavevector 𝑞 is generated in the presence of spin fluctuations. Subsequently, we can obtain 𝐴(𝑇) from the increase in free energy.

Specifically, we calculate 𝐴(𝑇) of Permalloy (Fe_0.2Ni_0.8) and L10-type FePt. For Fe_0.2Ni_0.8, the calculated magnetic moment is approximately 1 Bohr magneton (µ_B) at 𝑇 = 300 K, closely reproducing the measured values. The Curie temperature is approximately 550 K, slightly lower than the measured value (670 K). The obtained 𝐴(𝑇) falls within the range of values empirically used in the LLG equation (several meV/Å to 10 meV/Å), and 𝐴(𝑇) at room temperature appears to match well with the measured values. Additionally, 𝐴(𝑇) of FePt shows similar temperature dependence, aligning well with room temperature measurements. The results highlight the structure’s anisotropy, with significant directional dependence in 𝐴(𝑇).

Written by A. Sakuma