Quantum Hall Effect in Bulk (Multilayered) Organic Crystal
© The Physical Society of Japan
This article is on
Observations of ν = 1 Quantum Hall Effect and Inter-Band Effects of Magnetic Fields on Hall Conductivity in Organic Massless Dirac Fermion System α-(BETS)2I3 under Pressure
(JPSJ Editors' Choice)
J. Phys. Soc. Jpn. 92, 053701 (2023).
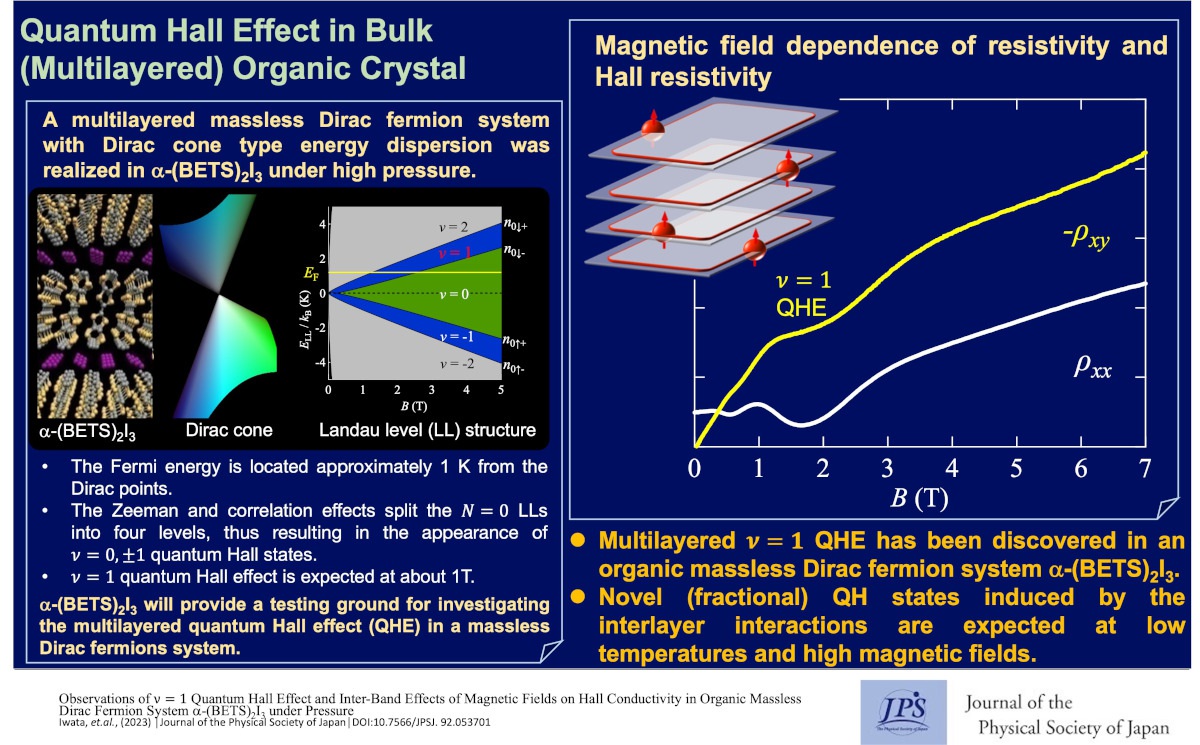
The multilayer quantum Hall effect is discovered in an organic massless Dirac electron system, α-(BETS)2I3 under pressure at low temperatures and a magnetic field of approximately 1 T.
Recently, topological materials have received considerable attention. Based on the topology concept, if a shape or space can be continuously deformed, then any shape changed by this continuous deformation can be considered identical. Well-known examples include the donut and mug, which are topologically identical in shape to a single hole, and whose number of holes characterizes their shape as topologically invariant.
A typical example of a topology is the quantum Hall effect (QHE). The QHE is a phenomenon observed primarily in two-dimensional (2D) electron systems under strong magnetic fields. The Hall conductivity is quantized as σxy=νe2/h in the region where the conductivity σxx=0, where the integer is the filling factor and can be regarded as topological invariant. The essence of the topological state in the quantum hall (QH) state is that the energy differences between the Landau levels result in an energy difference in the excitation of the bulk electrons. Another important feature is the appearance of a metallic state at the sample edge.
The fractional QHE has been discovered, in which is not an integer but a fraction with odd denominators (ν=1/3,2/3,1/5, ⋅⋅⋅). The interaction between electrons is crucial, and the fractional QHE is realized in 2D systems with extremely high mobility. In addition, in systems with Dirac fermions, a half-integer QHE with ν=N +1/2 per single spin and valley occurs, thus reflecting the -berry phase. This was first observed in monolayer graphene.
The QHE is typically observed in 2D systems at extremely low temperatures and high magnetic fields, whereas it rarely occurs in bulk (multilayered) crystals. Novel (fractional) QH states induced by interlayer interactions are expected in systems with strong electron correlations. Thus, the QHE in multilayered crystals with strong correlation should be investigated.
We successfully observed a QHE with ν=1 in an organic massless Dirac fermion system α-(BETS)2I3 under high pressure at low temperatures and a magnetic field of approximately 1 T.
One of the remarkable features of the Dirac fermion in solids is the emergence of a peculiar 𝑁 = 0 Landau levels, which do not undergo orbital motion even when a magnetic field is applied. All electrons are accommodated in the zero-energy state in a strong magnetic field. However, the Zeeman and correlation effects split the 𝑁 = 0 Landau levels into four levels; thus, ν= 0,±1 QH states appear.
The observation of the QHE with ν=1 a magnetic field of approximately 1 T suggests the high mobility of the system and that electron-electron interactions are important. A novel fractional QHE that reflects the interactions between layers is expected in this system.
(Written by N. Tajima on behalf of all authors)
Observations of ν = 1 Quantum Hall Effect and Inter-Band Effects of Magnetic Fields on Hall Conductivity in Organic Massless Dirac Fermion System α-(BETS)2I3 under Pressure
(JPSJ Editors' Choice)
J. Phys. Soc. Jpn. 92, 053701 (2023).
Share this topic
Fields
Related Articles
-
Exploring Electronic States in BEDT-TTF Organic Superconductors
Superconductivity
Electronic transport in condensed matter
Magnetic properties in condensed matter
2024-4-24
This review, published in the Journal of the Physical Society of Japan, provides a comprehensive summary of the electronic states observed in BEDT-TTF type organic superconductors, including metal-insulator transitions, Mottness transitions, non-Fermi liquids, quantum spin liquids, and Bose-Einstein condensation.
-
Conversion of Chiral Phonons into Magnons in Magnets
Electronic transport in condensed matter
2024-4-1
A new phenomenon involving the conversion of chiral phonons into magnons is theoretically predicted. The effective magnetic field induced by chiral phonons causes a change in the spin magnetization of magnets.
-
Variety of Mechanically Induced Spin Currents in Rashba Systems
Electronic transport in condensed matter
Magnetic properties in condensed matter
Structure and mechanical and thermal properties in condensed matter
2024-3-22
Various types of spin currents, including unconventional types, are generated in Rashba spin-orbit coupled systems by dynamic lattice distortions associated with, for example, surface acoustic waves.
-
What Determines the Sign of Spin Current? ~ Theoretical Study of Spin Seebeck Effect in Antiferromagnetic Insulators
Electronic transport in condensed matter
2024-3-18
We developed a microscopic theory for the spin Seebeck effect in antiferromagnets, that explains the sign reversal of the spin current at the spin-flop transition point and describes the sorts of dominant carriers.
-
Chiral Anomalies in Organic Dirac Semimetals
Electronic transport in condensed matter
2024-2-5
A three-dimensional massless Dirac fermion system exhibiting broken chiral symmetry was successfully realized in organic conductor α-(BEDT-TTF)2I3 under high pressures. Our study detected the chiral anomaly-induced negative magnetoresistance and planar Hall effects and opened new avenues for further advancements in the field.
