What Determines Non-Newtonian Flow Behavior in Glass-Forming Liquids?

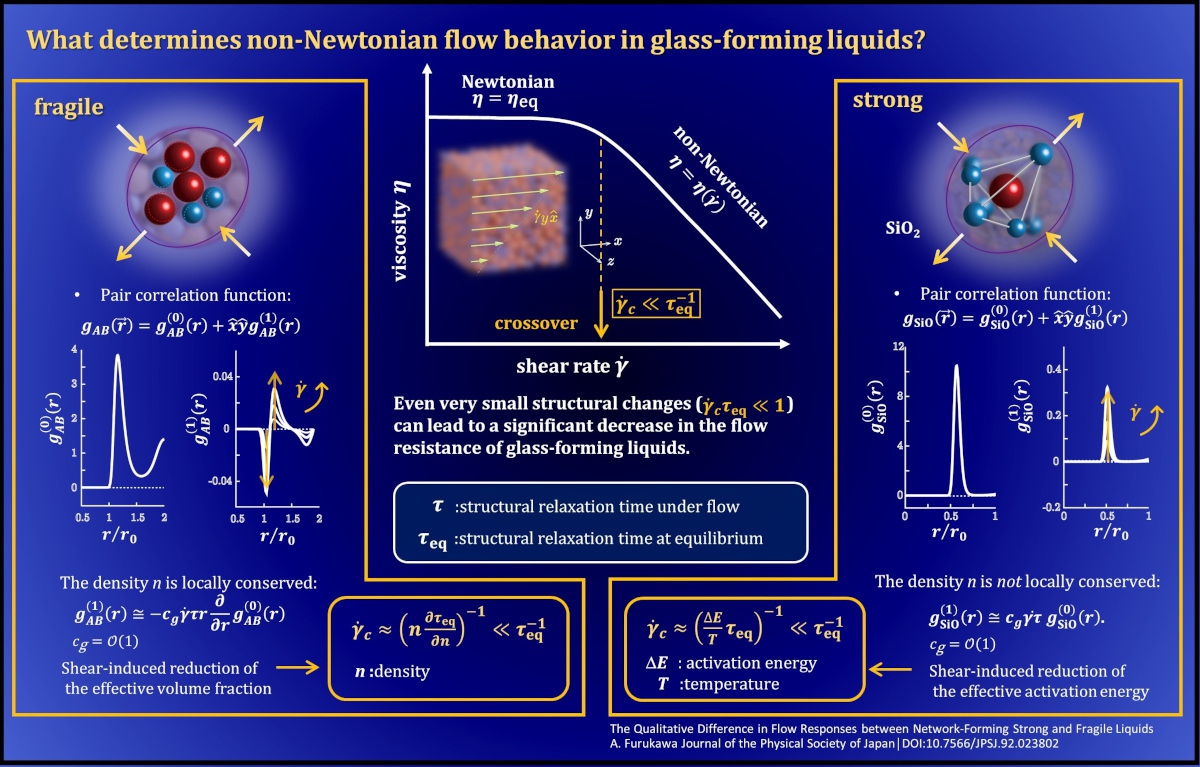
Shear thinning, where viscosity decreases as imposed shear rate increases, is one of the most ubiquitous non-Newtonian flow phenomena in various soft matter systems. One such system, a glass-forming liquid, exhibits significant shear thinning, but the underlying mechanism remains unclear.

When investigating the rheological properties of molecular or particulate fluids, the Péclet number defined as Pe = [advective transport rate]/[diffusive transport rate] is used to estimate the degree of departure from an equilibrium relaxation mechanism. In glass-forming liquids, the timescale of particle diffusion is usually identified with the structural relaxation time τ . Flows with Pe ~ Ýτ >1 indicate the dominance of advective effects over equilibrium structural relaxation mechanisms. Crossovers from Newtonian to non-Newtonian flow behaviors at Pe ~ 1 are observed in many soft matter systems, including polymers, liquid crystals, and critical fluids.

Therefore, similar crossovers might be expected to occur in glass-forming liquids. However, re-examining Pe at the onset of shear thinning in most simulations and experiments of glass-forming liquids indicates that shear thinning starts even when Pe is several orders of magnitude less than one. For Pe << 1, the flow effects are weak; the structural distortion induced by the applied flow is smaller than that induced by thermal fluctuations. This rheological feature of glass-forming liquids raises a question of why such tiny flow effects significantly alter the relaxation mechanism.

Extensive simulation studies have focused on the physical mechanism of shear-thinning behaviors; these studies mainly focused on fragile glass-forming liquids. However, there is another important class called strong glass-forming liquids. These two classes have distinct density and temperature dependencies on the structural relaxation time, indicating their distinct relaxation mechanisms. Therefore, although both strong and fragile liquids show similar shear-thinning behaviors, the two classes do not necessarily share a common underlying mechanism.

This paper provides possible new shear-thinning scenarios for ‘‘strong’‘ and ‘‘fragile’‘ glass-forming liquids; quantitative relationships between shear rate and viscosity reduction are derived and used to explain how and why viscosity can be significantly altered even at Pe<<1. The predictions agree with the molecular dynamics simulation results and readily apply to realistic problems, because they are expressed in terms of experimental observables. The shear thinning observed in glass-forming liquids often develop into more complex phenomena, like shear bands and fractures, which significantly modify the flow and mechanical properties of the system. Therefore, understanding the shear-thinning mechanism is essential for industrial applications in glassy materials production and processing, and for understanding large-scale volcanic phenomena like lava flows. This study enhances the understanding of such phenomena and advances the investigation of more complex nonlinear flow phenomena.