How Good is the Transition-State Theory?

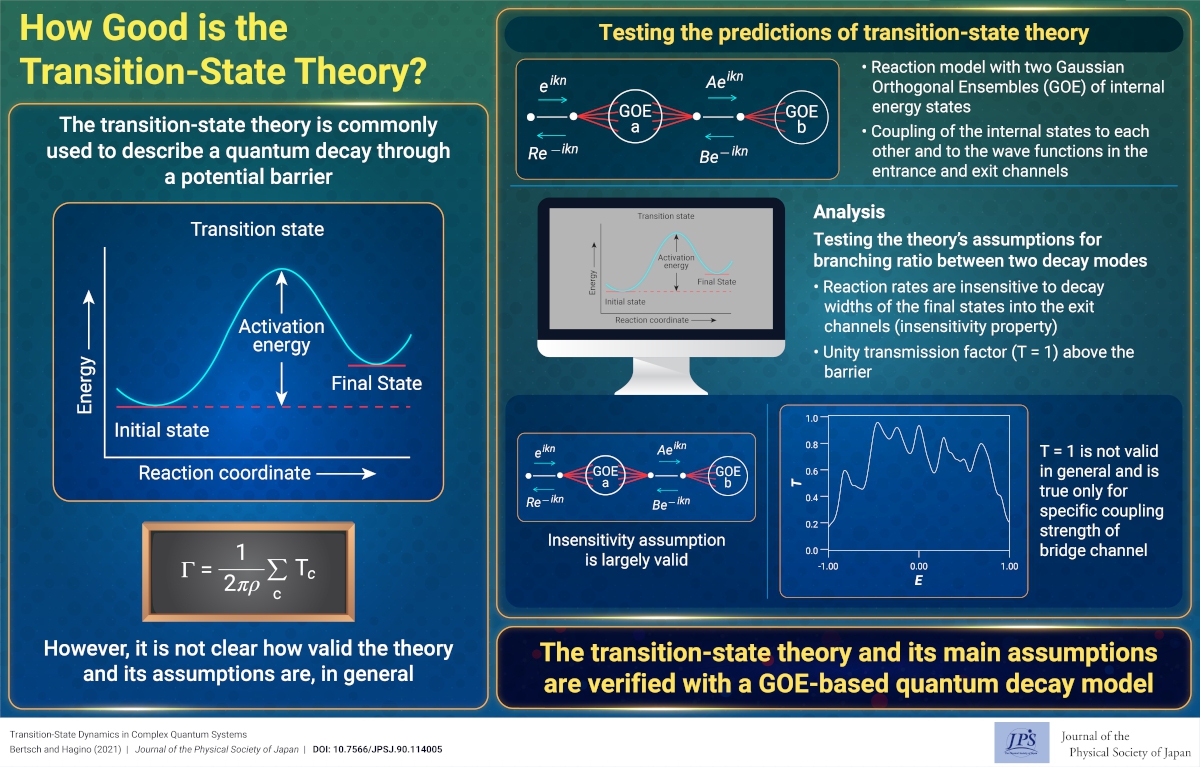
The decay of quantum systems through a potential barrier is ubiquitous in many fields of physics and chemistry, occurring in electron conduction within devices and quantum dots as well as chemical reactions, and nuclear fission. The usual framework for describing the barrier crossing is the "transition-state" theory, which was invented long ago to investigate chemical reactions and nuclear fission. The main assumption of this theory is that the decay rate is entirely determined at the highest point of the barrier and does not depend on what occurs afterward. This remarkable theory has been part of reaction theory since the 1930s and has been used in disciplines as widely distinct as chemistry and nuclear physics. However, this theory has not been validated for the quantum mechanics of many interacting particles.

In this study, a model was proposed to study reactions in systems with many interacting particles. The model allowed us to test whether the assumptions of the transition state theory could be satisfied in a full quantum theory. The model contains two reservoirs of internal states connected to each other by additional barrier-top states, and the reservoir states were considered using random matrix theory.

For the first time, we demonstrated that a main assumption of the transition-state theory can be easily satisfied by a more detailed theory, that is, the overall decay rate going through the far-side reservoir is largely determined by the barrier region and internal properties of the reservoirs, and is insensitive to the individual decay rates of the states out of the far-side reservoir.

In a subsequent paper (K. Hagino and G.F. Bertsch, Phys. Rev. E104, L052104(2021)), we applied the same model to discuss the variation of the decay rates between states. There is a well-established theory known as the Porter-Thomas distribution that has been validated for many systems, including atomic spectra, chemical reaction spectra, and nuclei. Surprisingly, our transition-state model revealed that this distribution differed depending on how large the individual rates were. The new distribution followed a different random matrix model, namely the Gaussian Unitary Ensemble, proposed by Dyson in 1960.
(Written by K. Hagino on behalf of all authors)