Which is Moving?—Pinning Down the Origin of Fluctuations in Muon Spin Relaxation—
© The Physical Society of Japan
This article is on
Distinguishing Ion Dynamics from Muon diffusion in Muon Spin Relaxation
(JPSJ Editors' Choice)
J. Phys. Soc. Jpn.
93,
044602
(2024)
.
The study demonstrated that we can distinguish between the diffusion motion of the muon itself and the motion of the surrounding ions in muon spin relaxation.
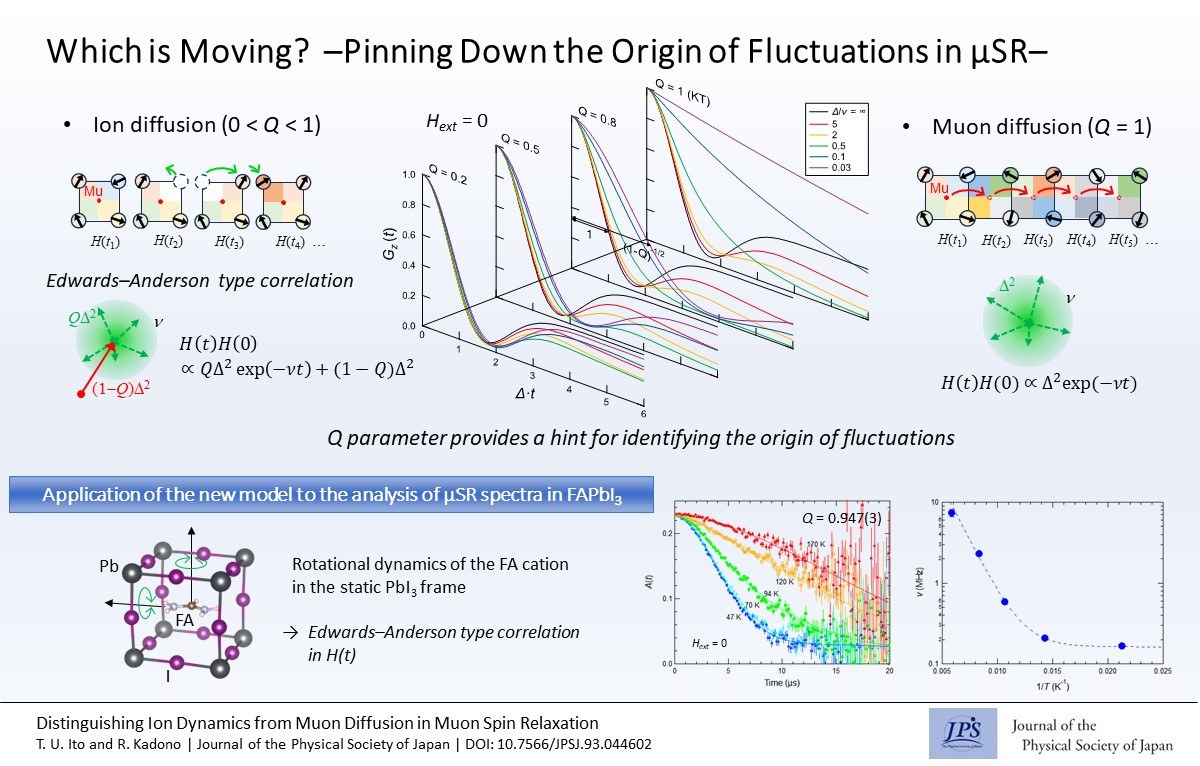
In the muon spin relaxation (µSR) measurements, the distribution (described by linewidth D) of internal magnetic field H(t) and its temporal fluctuations (with mean fluctuation rate n) can be observed by implanting spin-polarized muons into a material. However, distinguishing whether the fluctuations are caused by the diffusive motion of the muon itself or the motion of the ions around it, is difficult. In this study, by reviewing the strong collision model, which is an assumption used to describe spin relaxation, we observed that the difference in the cause of the fluctuation appeared as a difference in the spin relaxation function. The new model reproduces well the spin relaxation owing to the local rotational motion of cation molecules observed in hybrid perovskites; this opens the way to distinguish the cause of fluctuations solely from the µSR data.
When a muon exhibits jump-diffusion in a nonmagnetic material, the configuration of the nuclear magnetic moments around the muon changes simultaneously before and after the site change. The fluctuation of H(t) owing to these jumps is well approximated by the strong collision model [where the autocorrelation of H(t) is given by equation H(t)H(0)~D2exp(-nt)], and the time evolution of the muon spin polarization, Gz(t), is described by the dynamical Kubo–Toyabe (KT) relaxation function. However, if the H(t) fluctuations are due to the jump diffusion of ions, only a part of the ion configuration around the muon changes in one jump, and the strong collision model is not necessarily expected to be applicable.
Therefore, we performed Monte Carlo simulations for Gz(t) using a model in which the fluctuations of H(t) owing to ion motion were described by an Edwards–Anderson type autocorrelation function with the quasi-static and dynamic components of the autocorrelation separated by parameter Q [where H(t)H(0)~QD2exp(-nt) + (1-Q)D2], and Gz(t) was noted to deviate significantly from the KT function. To further verify this model, we compared the µSR spectra observed in the hybrid organic–inorganic perovskite FAPbI3 [FA refers to HC(NH2)2] with the simulation results. The least-squares curve fitting results showed excellent agreement with the model with Q = 0.947(3), yielding reasonable fluctuation frequencies for the dynamical component. This result opens the possibility of experimentally distinguishing between fluctuations owing to the dynamics of ions around muons and fluctuations owing to the self-diffusion of muons.
Written by T. U. Ito and R. Kadono
Distinguishing Ion Dynamics from Muon diffusion in Muon Spin Relaxation
(JPSJ Editors' Choice)
J. Phys. Soc. Jpn.
93,
044602
(2024)
.
Share this topic
Fields
Related Articles
-
Qualitative Changes in Kinetic Pathways Driven by Hydrodynamic Interactions in Dense Colloidal Suspensions
Cross-disciplinary physics and related areas of science and technology
Statistical physics and thermodynamics
Structure and mechanical and thermal properties in condensed matter
2025-4-18
Even in dense colloidal suspensions, where long-range hydrodynamic interactions are screened, near-field hydrodynamic interactions qualitatively influence the selection of kinetic pathways.
-
Exploring the Vibrant Interplay of Machine Learning and Physics
Cross-disciplinary physics and related areas of science and technology
Electron states in condensed matter
Elementary particles, fields, and strings
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Statistical physics and thermodynamics
Superconductivity
2025-3-13
This Journal of the Physical Society of Japan Special Topics edition explores how physics and machine learning complement each other and can solve unresolved problems in physics.
-
Bayesian Insights into X-ray Laue Oscillations: Quantitative Surface Roughness and Noise Modeling
Measurement, instrumentation, and techniques
Structure and mechanical and thermal properties in condensed matter
2025-2-14
This study adopts Bayesian inference using the replica exchange Monte Carlo method to accurately estimate thin-film properties from X-ray Laue oscillation data, enabling quantitative analysis and appropriate noise modeling.
-
Hyperuniform and Multifractal States in Bosonic Quasicrystalline Systems
Statistical physics and thermodynamics
Structure and mechanical and thermal properties in condensed matter
2025-2-10
Quantum states can be categorized as hyperuniform or multifractal based on electronic characteristics. This study demonstrates that bosonic quasicrystalline systems exhibit hyperuniform or multifractal quantum states.
-
Exploring Materials without Data Exposure: A Bayesian Optimizer using Secure Computation
Cross-disciplinary physics and related areas of science and technology
Measurement, instrumentation, and techniques
2025-2-6
Secure computation allows the manipulation of material data without exposing them, thereby offering an alternative to traditional open/closed data management. We recently reported the development of an application that performs Bayesian optimization using secure computation.




