A Closed Bosonic String Field Theory Based on the Fokker–Planck Formalism
© The Physical Society of Japan
This article is on
The Fokker–Planck formalism for closed bosonic strings
(PTEP Editors' Choice)
Prog. Theor. Exp. Phys. 2023, 023B05 (2023).
A string field theory for closed bosonic strings is formulated using pants decomposition and the Fokker–Planck formalism.
String theory is a framework where elementary particles and their interactions are replaced with strings as the basic building blocks of matter. Similar to how a particle sweeps out a worldline as it travels in spacetime, strings sweep out worldsheets as they move through spacetime. String field theory (SFT) is a formulation of string theory that reframes the dynamics of relativistic strings in terms of a quantum field theory. To construct an SFT, one must specify rules to cut the worldsheets into their fundamental units, namely propagators and vertices (Figure 1).

Figure 1
Unlike the particle theories, however, there are many choices for such rules and we can construct an SFT starting from one, in principle. The problem is that the SFT thus constructed becomes very complicated In general. The rule should, therefore, be carefully chosen to make for a simple SFT.
In this paper, I formulated an SFT for closed bosonic strings based on the “pants decomposition,” in which a bordered or punctured Riemann surface (describing a worldsheet for a closed bosonic string) can be decomposed into a pair of pants (Figure 2), which is analogous to three-string vertices. Every Riemann surface with a genus g and n punctures or boundaries admits a hyperbolic metric with a constant negative curvature if it satisfies the condition 2g - 2 + n > 0. This hyperbolic metric allows for a pants decomposition that, in turn, may be exploited to construct an SFT for closed bosonic strings.
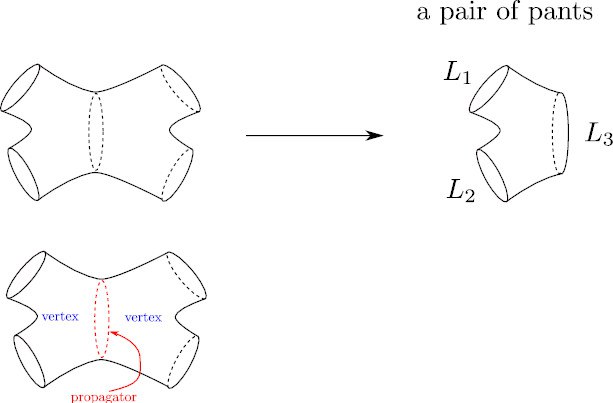
Figure 2
However, it was pointed out in the 1980’s that such an idea does not work. If one constructs the action for an SFT based on the pants decomposition, the amplitudes are expressed by integrals in which the fundamental domain of the modular group is covered infinite times, resulting in incorrect amplitudes.
In my paper, I circumvent this problem using Mirzakhani’s scheme for computing integrals over the moduli space of bordered Riemann surfaces. By applying this scheme, I derive a recursion relation satisfied by the off-shell amplitudes of closed bosonic strings. This recursion relation is related to the loop equations of minimal string theory, which can be described by an SFT through the Fokker–Planck formalism.
Accordingly, I convert the recursion relation into an SFT using a Fokker–Planck Hamiltonian consisting of kinetic terms and three-string vertices. However, the resulting SFT lacks the worldsheet BRST (Becchi-Rouet-Stora-Tyutin) symmetry. Fortunately, the theory can be made BRST invariant by introducing auxiliary fields.
This study thus offers an approach to constructing a simple action for closed bosonic string theory that uses the Fokker–Planck formalism instead of the traditional path integral formulation. Hopefully, this idea would open doors to constructing an SFT for superstrings.
The Fokker–Planck formalism for closed bosonic strings
(PTEP Editors' Choice)
Prog. Theor. Exp. Phys. 2023, 023B05 (2023).
Share this topic
Fields
Related Articles
-
Quantum Mechanics of One-Dimensional Three-Body Contact Interactions
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Theoretical Particle Physics
2024-2-13
The quantum mechanical description of topologically nontrivial three-body contact interactions in one dimension is not well understood. This study explores the Hamiltonian description of these interactions using the path-integral formalism.
-
Investigating Unitarity Violation of Lee–Wick’s Complex Ghost with Quantum Field Theory
Theoretical Particle Physics
2024-1-19
Theories with fourth-order derivatives like Lee–Wick’s quantum electrodynamics model or quadratic gravity result in complex ghosts above a definite energy threshold that violate unitarity.
-
Investigating Δ and Ω Baryons as Meson–Baryon Bound States in Lattice Quantum Chromodynamics
Theoretical Particle Physics
2023-7-13
We investigate Δ and Ω baryons as meson–baryon bound states in lattice quantum chromodynamics and show that their difference results from the kinematic structure of the two meson–baryon systems, and not their interaction.
-
Novel Insights Into Bulk Reconstruction in the Anti-de Sitter/Conformal Field Theory Correspondence
Theoretical Particle Physics
2023-6-1
Bulk reconstruction in anti-de Sitter/conformal field theory is fundamental to our understanding of quantum gravity. We show that contrary to popular belief, bulk reconstruction is rather simple and intuitive.
-
The Stolz–Teichner Conjecture and Supermoonshine
Theoretical Particle Physics
2023-4-25
We check the validity of the "divisibility property," predicted by the Stolz–Teichner conjecture, for several infinite families of theories built from Duncan’s Supermoonshine module. Along the way, we develop the tools necessary to construct the so-called "periodicity class."
