Spin-Orbit Coupled Electrons on Kagome Lattice Give Rise to Various Magnetic Orderings
© The Physical Society of Japan
This article is on
Magnetic Orderings from Spin-Orbit Coupled Electrons on Kagome Lattice
(JPSJ Editors' Choice)
J. Phys. Soc. Jpn. 91, 083702 (2022).
Diverse magnetic orderings are found to be produced by spin-orbit coupled electrons on the kagome lattice. This finding provides a unified guiding principle for the design of magnetic topological materials.
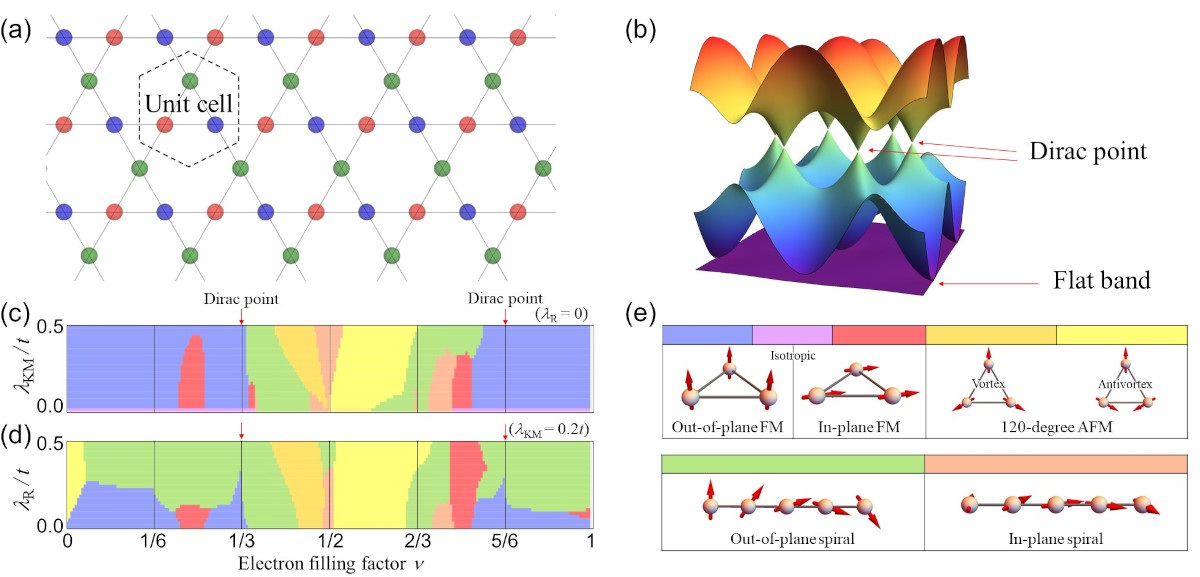
Fig. 1: (a) Kagome lattice. The unit cell consists of three sublattices. (b) Electronic band structure with linear band touching points (Dirac points) and flat band. (c)(d) Obtained magnetic phase diagrams with spin-orbit couplings and electron filling factor v. The spin-orbit couplings (Rashba type λR and Kane-Mele type λKM) are scaled by the nearest-neighbor hopping amplitude t on the kagome lattice. (e) Legends of magnetic orderings. Panels (c)-(e) are adapted from Fig. 1 of J. Phys. Soc. Jpn. 91, 083702 (2022).
The kagome lattice [Fig. 1(a)] is one of the typical structures realized in two-dimensional or layered materials. The study of the kagome lattice has a long history in the context of magnetism; the kagome lattice exhibits geometrical frustrations, which can give rise to various magnetic orderings. The recent discovery of topological features in the electronic band structure, known as a “Dirac point” or “Weyl point” [see Fig. 1(b)], of kagome layered materials renewed the interest in kagome lattices. For example, Mn3Sn shows in-plane 120-degree antiferromagnetic ordering and exhibits Weyl points in the electronic bands. Co3Sn2S2 also has Weyl points, whereas it shows out-of-plane ferromagnetic ordering. Fe3Sn2 exhibits in-plane ferromagnetic ordering, yet its electronic bands exhibit massive Dirac dispersion. However, a unified understanding of the relationship between the magnetism and topological electronic states has not yet been established.
This study clarified the connection between these magnetic orderings and topological electronic structures in terms of spin-orbit couplings. Spin-orbit coupling is the relativistic interaction between the electron motion and electron spin, and plays an important role in realizing topological band structures. The magnetic phase diagrams of a kagome monolayer were numerically obtained by introducing spin-orbit coupling in a model of the electron system coupled with localized spins (Kondo lattice model). The ground state magnetic ordering that minimizes the energy of the electron system depends on the electron filling factor and strength of spin-orbit couplings. Typical spin-orbit couplings resulting from the inversion symmetry breaking of the kagome lattice, namely the Rashba (λR) and Kane-Mele (λKM) types, were considered. As shown in Figs. 1(c) and 1(d), various magnetic orderings, such as ferromagnetic, 120-degree antiferromagnetic, and magnetic spirals [see Fig. 1(e)], are realized. These magnetic orderings are related to the topological band structures in the kagome lattice; the ordering varies as the electron filling factor passes through the bandgap at the Dirac points opened by the spin-orbit couplings. Noncollinear orderings, such as 120-degree antiferromagnetic and spiral orderings, are also governed by the effective Dzyaloshinskii-Moriya interaction of spins due to the spin-orbit couplings.
Because both the electron filling factor and spin-orbit couplings can be controlled by the substitution of elements, the obtained phase diagrams may be helpful for understanding the effects of the substitution on the magnetic orderings in various kagome materials. These findings provide a unified guiding principle for material design and will greatly accelerate the search for magnetic topological materials for device applications.
(Written by Y. Araki, K. Kobayashi, and A. Ozawa on behalf of all authors).
Magnetic Orderings from Spin-Orbit Coupled Electrons on Kagome Lattice
(JPSJ Editors' Choice)
J. Phys. Soc. Jpn. 91, 083702 (2022).
Share this topic
Fields
Related Articles
-
Antiferromagnetism Induces Dissipationless Transverse Conductivity
Electronic transport in condensed matter
Magnetic properties in condensed matter
Electronic structure and electrical properties of surfaces and nanostructures
2024-7-24
An investigation using high-quality NbMnP crystals demonstrates that the anomalous Hall conductivity arising from antiferromagnetism is dissipationless, as expected from the intrinsic mechanism.
-
Towards Uncovering the Hidden Order of URu2Si2 Phase Transition
Magnetic properties in condensed matter
Electronic structure and electrical properties of surfaces and nanostructures
2024-1-11
We propose a chiral charge as the hidden order parameter in URu2Si2 and present experiments to detect it by focusing on breakings of mirror and inversion symmetries at the local uranium ion.
-
Possible Origin of High Thermoelectric Power Factor in Ultrathin FeSe: A Two-band Model
Electronic structure and electrical properties of surfaces and nanostructures
Structure and mechanical and thermal properties in condensed matter
Cross-disciplinary physics and related areas of science and technology
2023-12-21
The high thermoelectric power factor observed in ultrathin FeSe can be theoretically explained by a two-band model with chemical potential between upper and lower band bottoms.
-
How Many Excitons Can Combine?
Dielectric, optical, and other properties in condensed matter
Electronic structure and electrical properties of surfaces and nanostructures
2023-8-31
Quantum diffusion Monte Carlo simulation demonstrated the formation of polyexcitons in two-dimensional multi-valley semiconductor systems, where all exciton pairs were energetically bound by equal-strength “chemical bonds.”
-
Topological Properties of the Periodic Toda Lattice: Analogy with the Thouless Pump
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Electronic structure and electrical properties of surfaces and nanostructures
2023-8-8
We find that the periodic Toda lattice belongs to the same topological class as the Thouless pump.
