Economic Irreversibility: The Universal Guiding Principle of Infection Control
© The Physical Society of Japan
This article is on
Economic Irreversibility in Pandemic Control Processes: Rigorous Modeling of Delayed Countermeasures and Consequential Cost Increases
J. Phys. Soc. Jpn. 90, 114007 (2021).
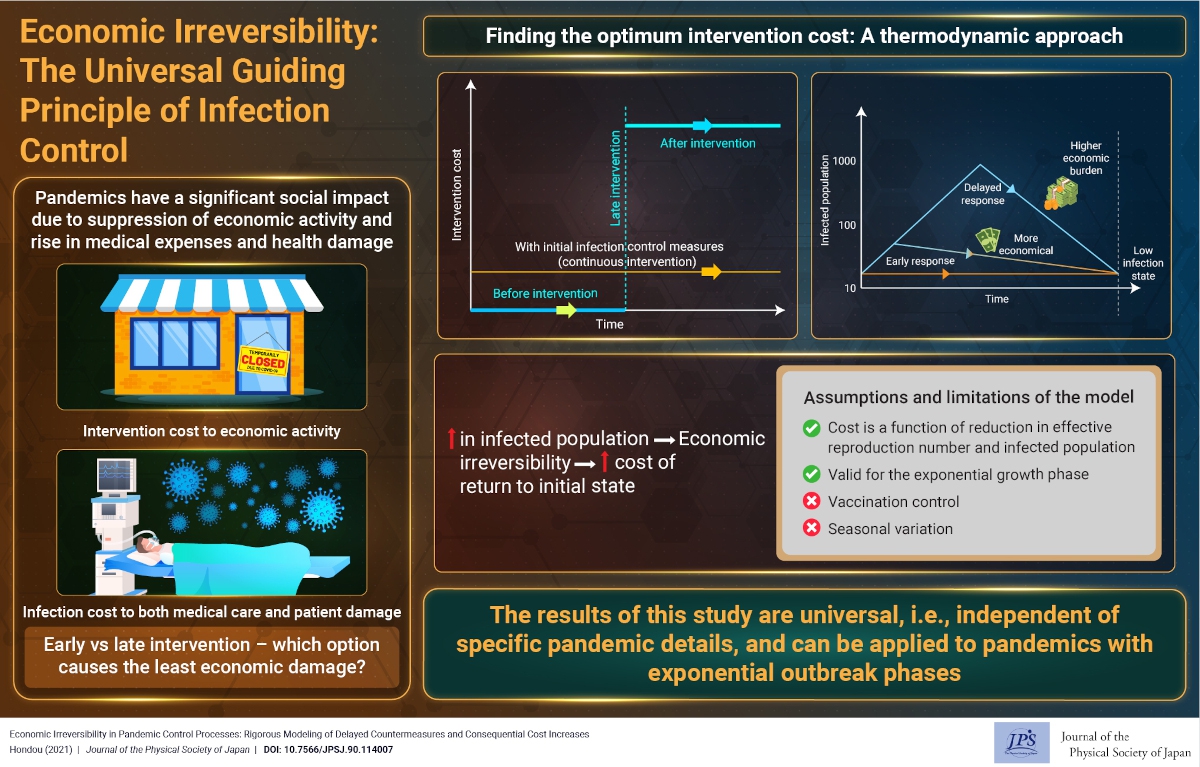
It is preferable to avoid lockdowns, as lockdowns at seriously spread phases are very expensive. It would be economically better to utilize less intense countermeasures as early as possible to avoid lockdowns in later phases.
Since the early 2020, governments across the globe have grappled with preventing the spread of COVID-19 and mitigating the economic impacts of this deadly virus. Several debates have raged over the methods to balance stringent infection control while maintaining a sense of economic normalcy.
In this study, theories of thermodynamics have been used to generate a new concept termed as "economic irreversibility." It contends that delaying infection control measures is additionally expensive in the long run.
Although, certain economists have utilized a cost-benefit analysis to argue for timely intervention, its universal applicability remains questionable. This is because previous studies have been performed using numerical simulations that include investigating specific situations with given parameters the results of which depend on the socio-economic conditions and on the characteristics of the infectious agents.
To further develop a universal guiding principle to control pandemics, the author’s experience in thermodynamics is utilized.
A cost-benefit analysis is an optimization problem similar to exploring more efficient thermal cycles in thermodynamics. The benefit and cost are the reduction in infections, and the economic damage caused by the countermeasure, respectively. The efficiency of the countermeasure processes are theoretically compared with the same period in which the initial and the final infection status (the number of infected persons) remain the same.
The application of economic irreversibility showed that the delay in infection control results in increased costs and contradicts the idea that infection control translates into economic damage. In terms of thermodynamics, it can be said that early countermeasures render the situation more reversible.
Furthermore, this study did not require adjusting for different infectious diseases or socio-economic conditions, making it applicable on a wider scale. It can be applied to the current COVID-19 pandemic or probable future ones, regardless of whether “herd immunity” exists or not. To the best of the author’s knowledge, this is the first analytical study of the economic efficiency during pandemic control.
The validity of the present study is subject to the assumptions of the methodology. In this study, two principal assumptions have been made:
1. |
The intervention cost depends on the effective reproduction number, and its cost function is concave as to the effective reproduction number. |
2. |
The epidemic is in the infection-spreading phase and thus the infected population increases and decreases while obeying exponential dynamics. |
It is assumed that countermeasures are utilized in order corresponding to their cost-effectiveness. Moreover, exponential dynamics is a common feature of pandemics. Thus, the results are not restricted to a specific model; however, they demonstrate the basic underlying characteristics of pandemic countermeasures.
(Written by T. Hondou)
Economic Irreversibility in Pandemic Control Processes: Rigorous Modeling of Delayed Countermeasures and Consequential Cost Increases
J. Phys. Soc. Jpn. 90, 114007 (2021).
Share this topic
Fields
Related Articles
-
Which is Moving?—Pinning Down the Origin of Fluctuations in Muon Spin Relaxation—
Structure and mechanical and thermal properties in condensed matter
Cross-disciplinary physics and related areas of science and technology
2024-3-28
The study demonstrated that we can distinguish between the diffusion motion of the muon itself and the motion of the surrounding ions in muon spin relaxation.
-
Thermodynamic Property of a CMOS Device beyond Landauer Limit
Statistical physics and thermodynamics
Electronic transport in condensed matter
Cross-disciplinary physics and related areas of science and technology
2024-1-23
Focusing on a CMOS NAND GATE operating in a sub-threshold region, the thermodynamic cost of computation was analyzed in relation to input/output voltages surpassing the Landauer limit.
-
Possible Origin of High Thermoelectric Power Factor in Ultrathin FeSe: A Two-band Model
Electronic structure and electrical properties of surfaces and nanostructures
Structure and mechanical and thermal properties in condensed matter
Cross-disciplinary physics and related areas of science and technology
2023-12-21
The high thermoelectric power factor observed in ultrathin FeSe can be theoretically explained by a two-band model with chemical potential between upper and lower band bottoms.
-
Exploring Recent Advances in the Physics of Biofluid Locomotion
Measurement, instrumentation, and techniques
Cross-disciplinary physics and related areas of science and technology
Electromagnetism, optics, acoustics, heat transfer, and classical and fluid mechanics
Statistical physics and thermodynamics
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Structure and mechanical and thermal properties in condensed matter
2023-12-8
This Special Topics Edition of the JPSJ describes the latest advances in the field of biofluid locomotion, shedding light on the underlying physics behind the movement of organisms that swim and fly.
-
A New Superconductor Family with Various Magnetic Elements
Superconductivity
Cross-disciplinary physics and related areas of science and technology
Electron states in condensed matter
2023-10-27
A new superconductor family, Sc6MTe2, has been discovered, comprising seven variations with magnetic elements labeled as M. Notably, only a few known superconductor families exist that involve various magnetic elements.