View larger image

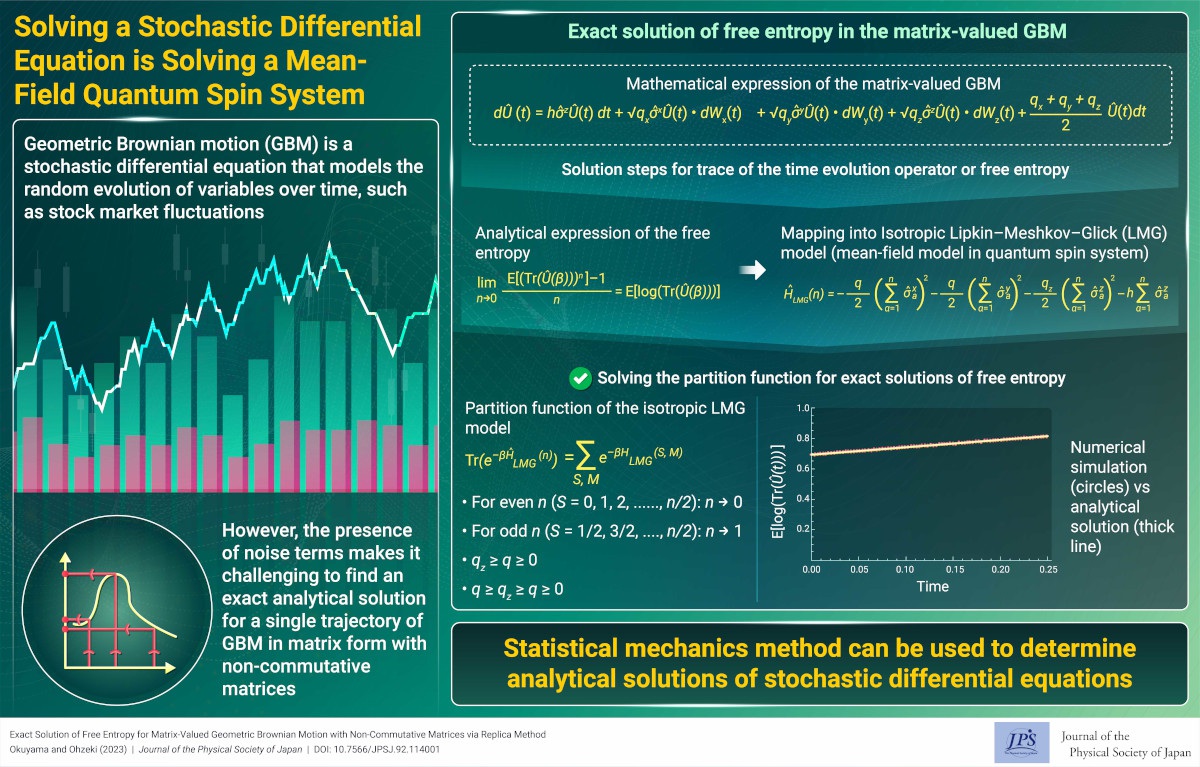
Stochastic differential equations are differential equations where stochastic terms are introduced. Stochastic differential equations were originally introduced by Einstein in research on Brownian motion and are now used not only in mathematics and physics, but also in various fields such as financial engineering. In many cases, solving stochastic differential equations analytically is extremely difficult compared to solving ordinary differential equations, and solving stochastic differential equations numerically also incurs a much higher cost than solving ordinary differential equations.

Our research attempts to obtain analytical solutions for stochastic differential equations. Geometric Brownian motion is one of the most famous stochastic differential equations for which analytical solutions have been obtained. Geometric Brownian motion is used in financial engineering option pricing models. Geometric Brownian motion can be regarded as an ordinary first-order linear homogeneous differential equation, in which the coefficients are replaced by stochastic noise. The exact solution of the geometric Brownian motion can be easily obtained in the same manner as an ordinary first-order homogeneous linear differential equation can be easily solved.

What happens when we consider multivariable geometric Brownian motion? In the case of ordinary differential equations, multivariable first-order homogeneous linear differential equations can be solved by diagonalizing the matrices. However, for multivariable geometric Brownian motion, this problem becomes extremely difficult, and when there is more than one stochastic noise, multivariable geometric Brownian motion cannot be solved by diagonalization. In other words, it has been believed that it is impossible to obtain an exact solution for multivariable geometric Brownian motion.

Under these circumstances, we considered a 2x2 matrix-valued geometric Brownian motion to be the simplest and most nontrivial multivariable geometric Brownian motion. As explained above, it is difficult to solve the 2x2 matrix-valued geometric Brownian motion using the conventional method. Instead, we applied the replica method developed in the spin-glass theory of statistical physics (which is closely related to the Nobel Prize in Physics awarded to Parisi in 2021). The replica method analyzes a model with randomness by mapping it onto an effective model without randomness.

Using the replica method, we found that the time-evolution operator of the matrix-valued geometric Brownian motion can be mapped to the partition function of a mean-field quantum spin system called the Lipkin-Meshkov-Glick model, which was originally proposed in nuclear physics. Furthermore, by analyzing the partition function of the Lipkin-Meshkov-Glick model, we succeeded in obtaining analytical solutions for various quantities of matrix-valued geometrical Brownian motion.

In summary, by analyzing a mean-field quantum spin system, we obtained exact solutions for various quantities of matrix-valued geometric Brownian motion that was previously thought to be unsolvable. Our results imply that there is a close connection between matrix-valued geometric Brownian motion and a mean-field quantum spin system, which, at first glance, have nothing to do with each other.

Written by Manaka Okuyama on behalf of all authors