View larger image

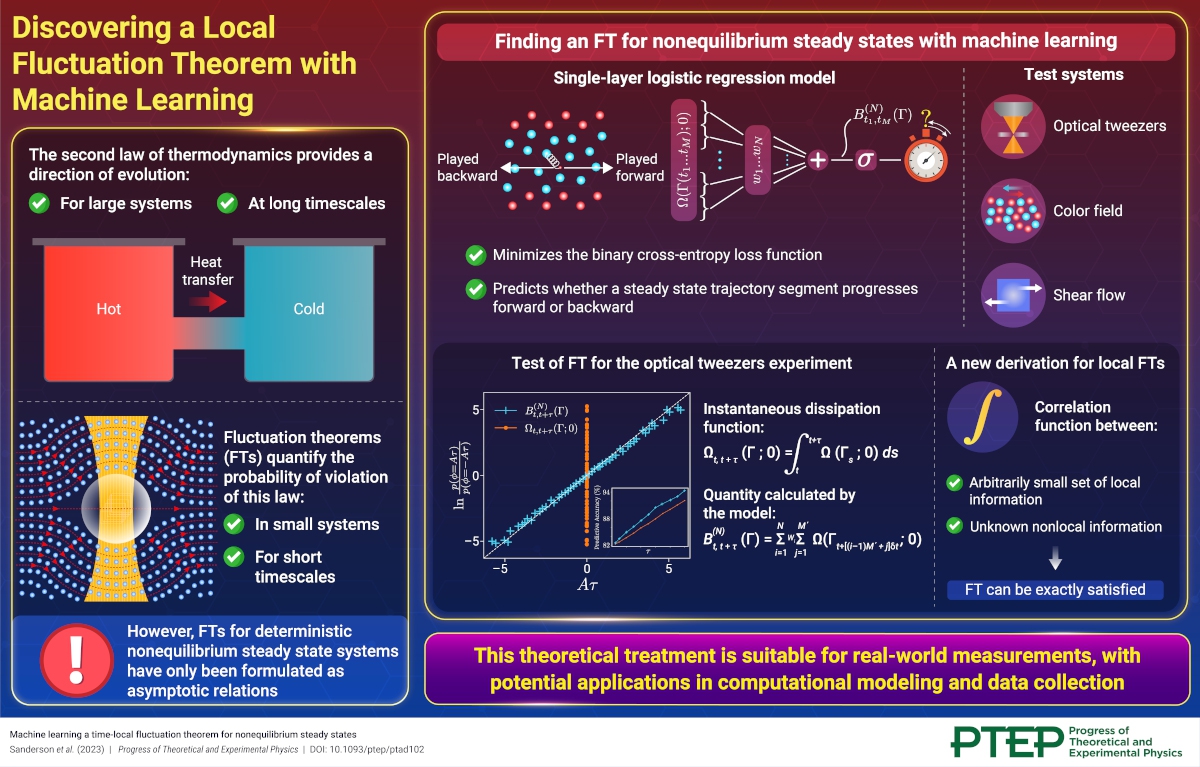
The second law of thermodynamics states that for large systems, there is a direction associated with their evolution over large time scales. However, in the realm of nonequilibrium dynamics, especially where a system is driven far from equilibrium, understanding and quantifying thermodynamic relations is challenging.

In this regard, fluctuation theorems (FTs), which quantify the thermodynamic reversibility of a system in terms of a dissipation function, have emerged as an essential tool for characterizing the probability of observing events in small systems during short timescales that violate the second law of thermodynamics. However, these theorems have only been formulated for a limited class of systems.

Consequently, our understanding of deterministic nonequilibrium steady states—a system with unknown phase space distribution for which only asymptotic FTs hold— remains limited. This is because all attempts to evaluate their dissipation function require either the trajectory segment of interest to be relatively long or information about the entire trajectory around that segment.

In this study, we addressed this long-standing problem in statistical mechanics by utilizing a simple machine learning model. The model was trained to minimize the binary cross-entropy loss function and discern whether a segment of a steady state trajectory progresses forward or backward in time. This yielded a function that satisfied an FT and relied only upon the information within the segment of interest.

Remarkably, this time-local FT is applicable even to extremely short trajectory segments and holds true for systems far from equilibrium as well as for various nonequilibrium dynamics, surpassing all previously known theoretical approximations.

We further demonstrated that any model reaching the global minimum of the binary cross-entropy loss function must be a well-calibrated predictor of time’s arrow and satisfy an FT. This leads us to a new derivation for local-time FTs: an FT can be exactly satisfied for an arbitrarily small set of local information provided the correlation function between that information and the unknown, non-local information is known.

Since our theoretical treatment is applicable to feasible real-world measurements, which only capture information from a local region and for a finite duration, it could potentially have wide-ranging applications in computational modeling as well as real-world data collection.

Consequently, this study could eventually lead to an enhanced understanding of nonequilibrium steady state systems across diverse fields, including fluid dynamics, heat transfer, semiconductor operation, ion transport, biology, and climate modeling.