View larger image

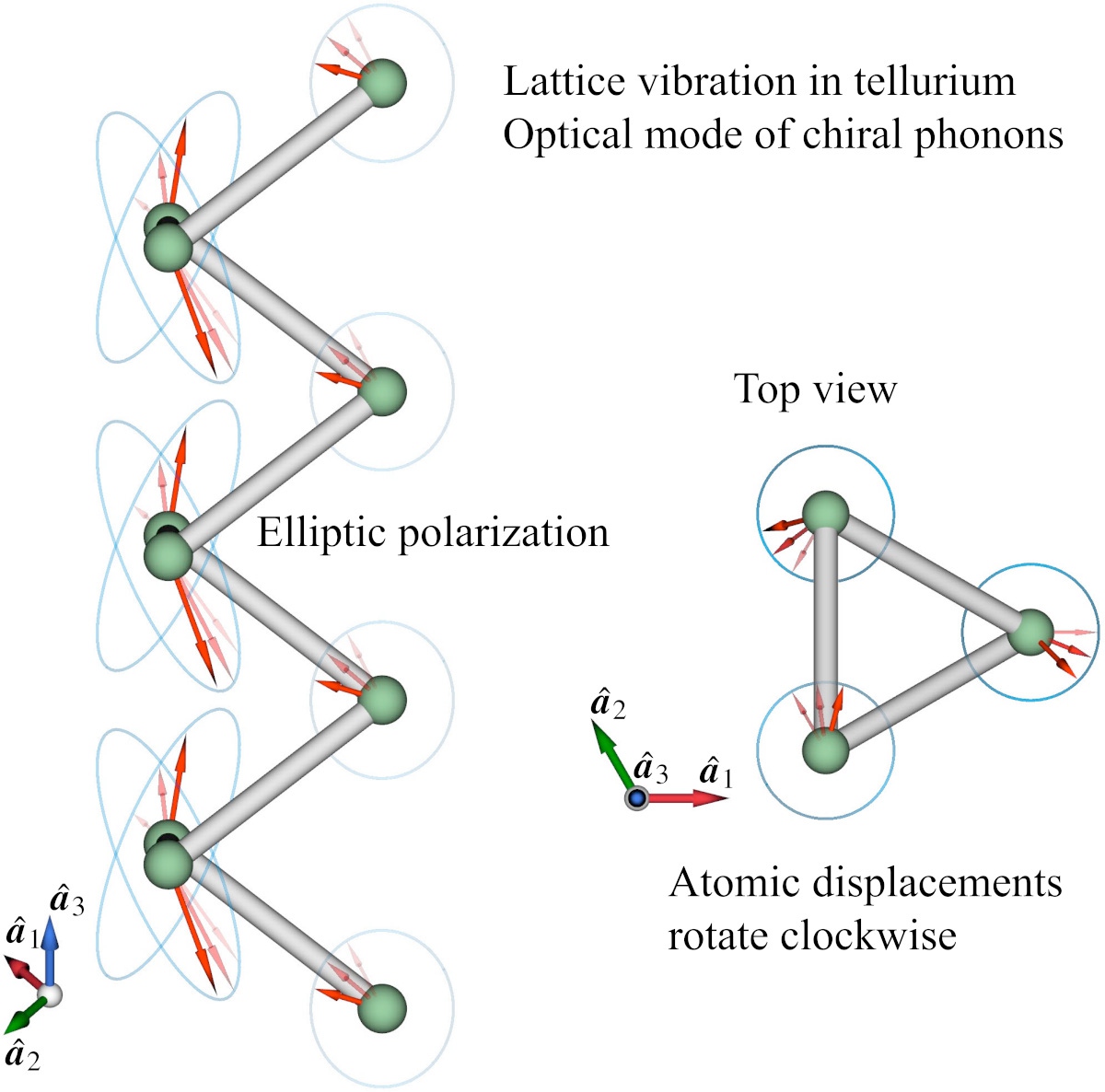
Propagating lattice vibration in crystals resembles light, and atomic displacement corresponds to the electric or magnetic field. One can easily control light by using a waveplate to convert its polarization from linear to circular and vice versa without changing the frequency of light. However, this type of conversion is not possible for lattice vibrations in chiral crystals, such as quartz and tellurium. This is because some vibration modes must have a distorted circular (i.e., elliptic) polarization, and their eigenfrequency depends on whether displacements rotate clockwise or anticlockwise in contrast to the behavior of ordinary light. The quanta of these vibration modes are called chiral phonons, and the corresponding eigenfrequency determines their energy. Chiral crystals have a structure with definite handedness. The mirror image of the structure is not identical to the original, as the right-handed screw differs from the mirror-reflected left-handed screw. The abovementioned split of the chiral phonon energy is an important consequence of the chiral lattice structure.

The crystals have multiple branches of lattice vibrations, i.e., phonons; three are acoustic branches, while the others are optical. One crucial question is which branch is most sensitive to the chiral structure. By studying a chiral model with a screw structure, the authors have shown that the optical branches are considerably more sensitive than the acoustic branches and obtained a simple formula for the energy splitting between chiral phonons rotating oppositely. The splitting is proportional to the product of the phonon’s linear momentum and the intrinsic angular momentum representing the rotation direction. The proportionality constant Γ is an important order parameter characterizing the system’s chirality, and its explicit form has been obtained in this work as a function of microscopic material parameters. As the chiral systems lack mirror and related inversion symmetries, polar vectors such as linear momentum can directly couple to axial vectors such as angular momentum, and their coupling constants have the symmetry of pseudoscalar. The nonvanishing value of the obtained Γ demonstrates this situation and is related to the electric toroidal monopole G₀. As for the chiral acoustic branches, there has been an argument that they may have different sound velocity values depending on the phonon’s angular momentum. The authors have proved that these sound velocities should be identical under general conditions. They have also obtained conditions for microscopic models, which are expected to be useful for model building based on the first-principle calculations.

(written by H. Tsunetsugu on behalf of all the authors.)