-
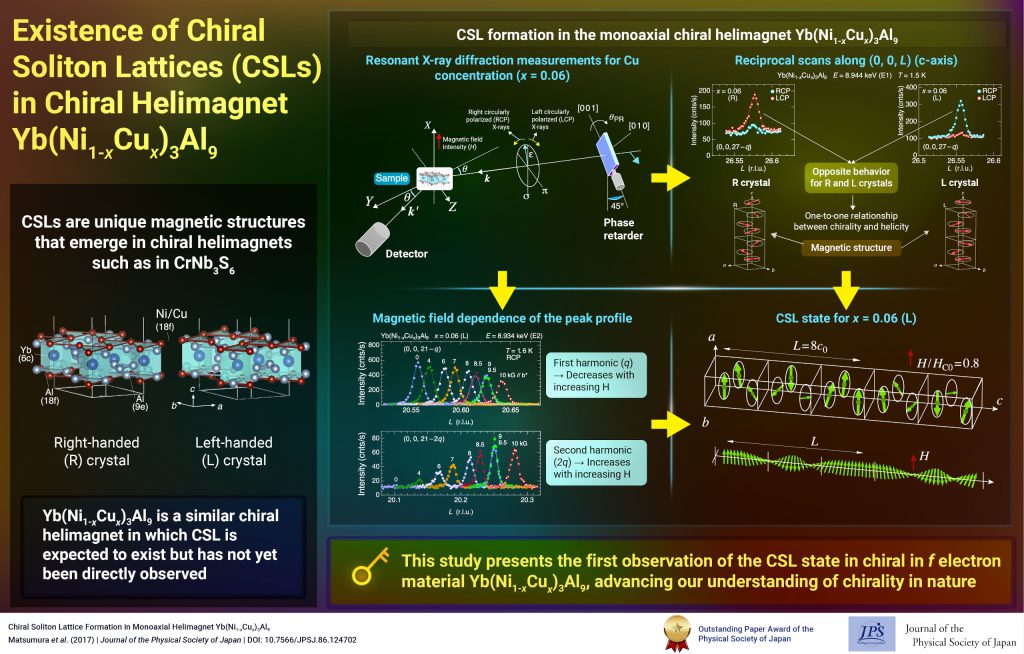
Existence of Chiral Soliton Lattices (CSLs) in Chiral Helimagnet Yb(Ni1-xCux)3Al9
2025-4-1
Our study examines the magnetic structure of the monoaxial chiral helimagnet Yb(Ni1-xCux)3Al9, providing first direct evidence of the formation of chiral soliton lattice state.
Magnetic properties in condensed matter
-
PICKUP
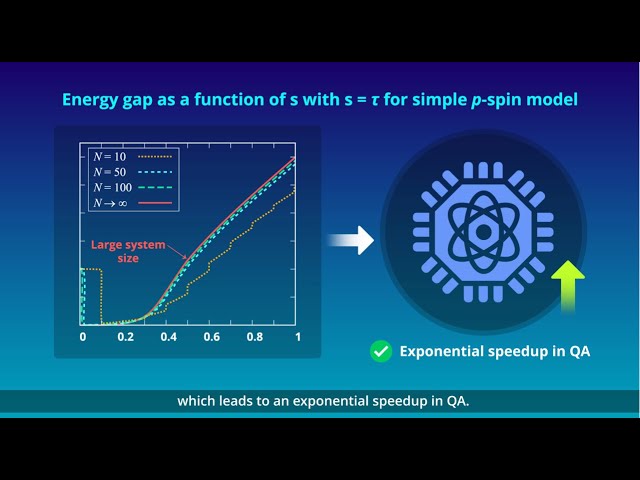
Overcoming Phase Transitions for Faster Quantum Annealing
2025-3-27
This study presents an innovative method to address the problem of phase transitions in quantum annealing, resulting in an exponential speedup of the process.
Statistical physics and thermodynamics
-
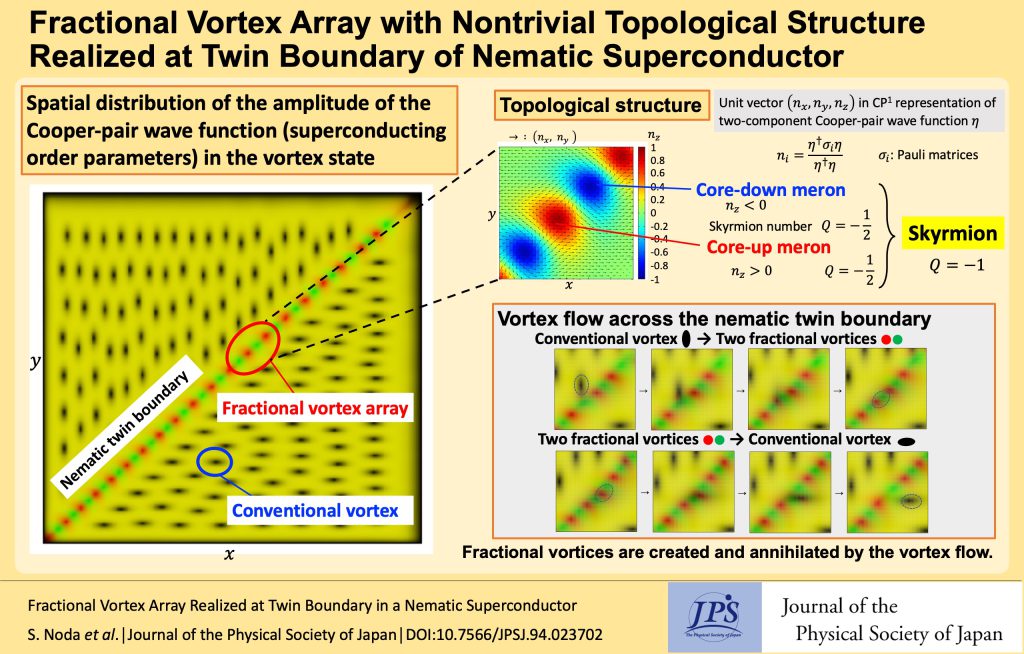
Fractional Vortex Array with Nontrivial Topological Structure Realized at Twin Boundary of Nematic Superconductor
2025-3-24
Analysis of the two-component Ginzburg-Landau theory suggests that a conventional vortex is transformed into two fractional vortices with the topological nature of core-down and core-up merons at the twin boundary of a nematic superconductor.
Superconductivity
-
PICKUP
Exploring the Vibrant Interplay of Machine Learning and Physics
2025-3-13
This Journal of the Physical Society of Japan Special Topics edition explores how physics and machine learning complement each other and can solve unresolved problems in physics.
Cross-disciplinary physics and related areas of science and technology
Electron states in condensed matter
Elementary particles, fields, and strings
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Statistical physics and thermodynamics
Superconductivity
-
PICKUP
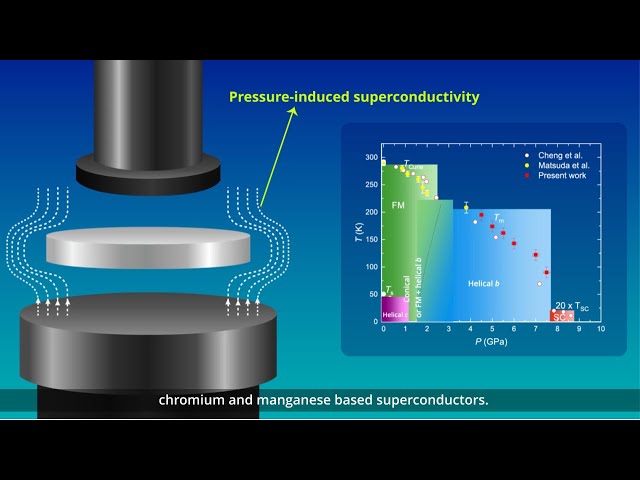
Understanding Pressure-Induced Superconductivity in CrAs and MnP
2025-3-10
This study reviews existing research on the pressure-induced variation of magnetic properties of transition metal mono-pnictides like CrAS, MnP, and others, aiming to understand the unconventional superconductivity observed in CrAs and MnP.
Magnetic properties in condensed matter
-
PICKUP
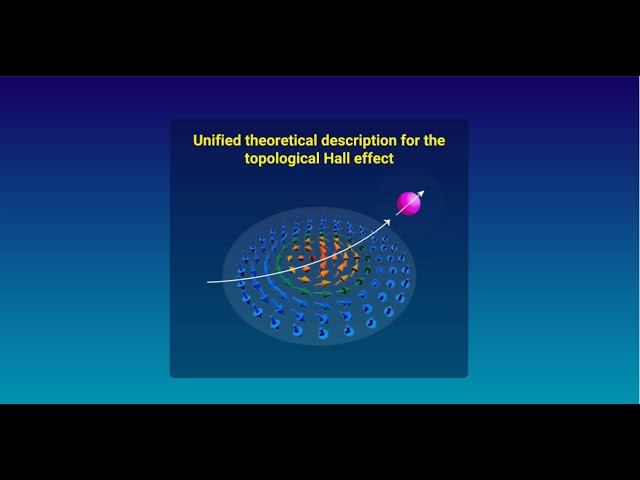
A Unified Theory of Topological Hall Effect
2025-3-6
This paper presents a unified theoretical description for the topological Hall effect, covering the entire region from strong- to weak-coupling, extending its picture beyond the Berry phase.
Electronic transport in condensed matter
-
PICKUP
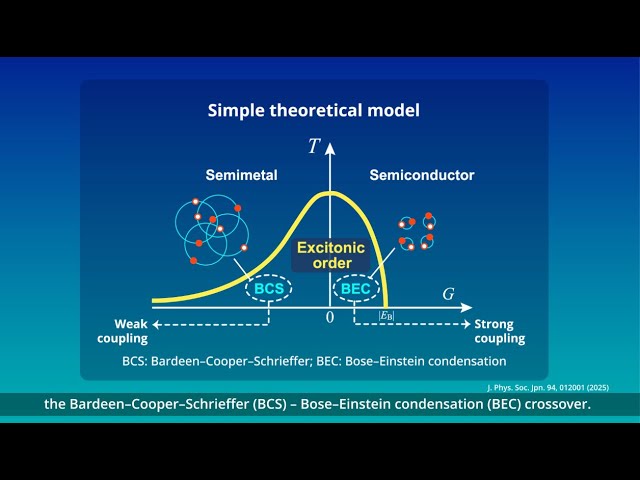
Excitonic Insulators: Challenges in Realizing a Theoretically Predicted State of Matter
2025-3-3
The realization of an excitonic insulator can help in the establishment of a new electronic state in condensed matter physics, one that has the potential to exhibit novel electric, magnetic, and optical responses beyond those of conventional materials.
Electron states in condensed matter
Electronic transport in condensed matter
-
PICKUP

Characterizing Quantum Chaos: Exact Analytical Expression for Gap Ratio Distribution
2025-2-27
This study presents the exact analytical expressions for gap ratio distribution, which is widely used to measure the chaoticity of quantum systems in many-body systems.
General and Mathematical Physics
-
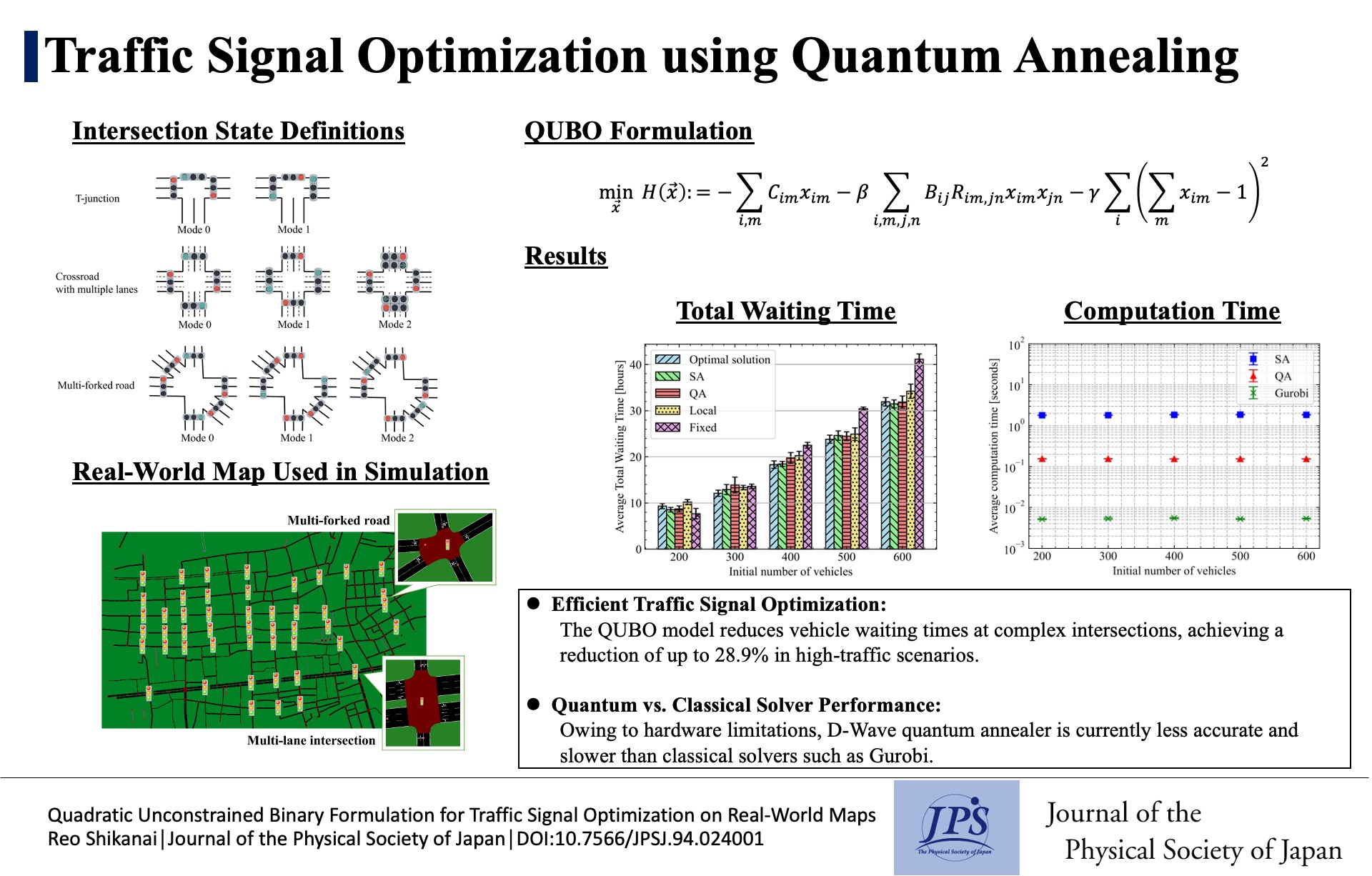
Traffic Signal Optimization using Quantum Annealing
2025-2-25
This paper introduces a QUBO model for traffic signal optimization on real-world maps. Using D-Wave quantum annealing and SUMO simulations, the model reduces vehicle waiting times, but underperforms classical solvers.
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
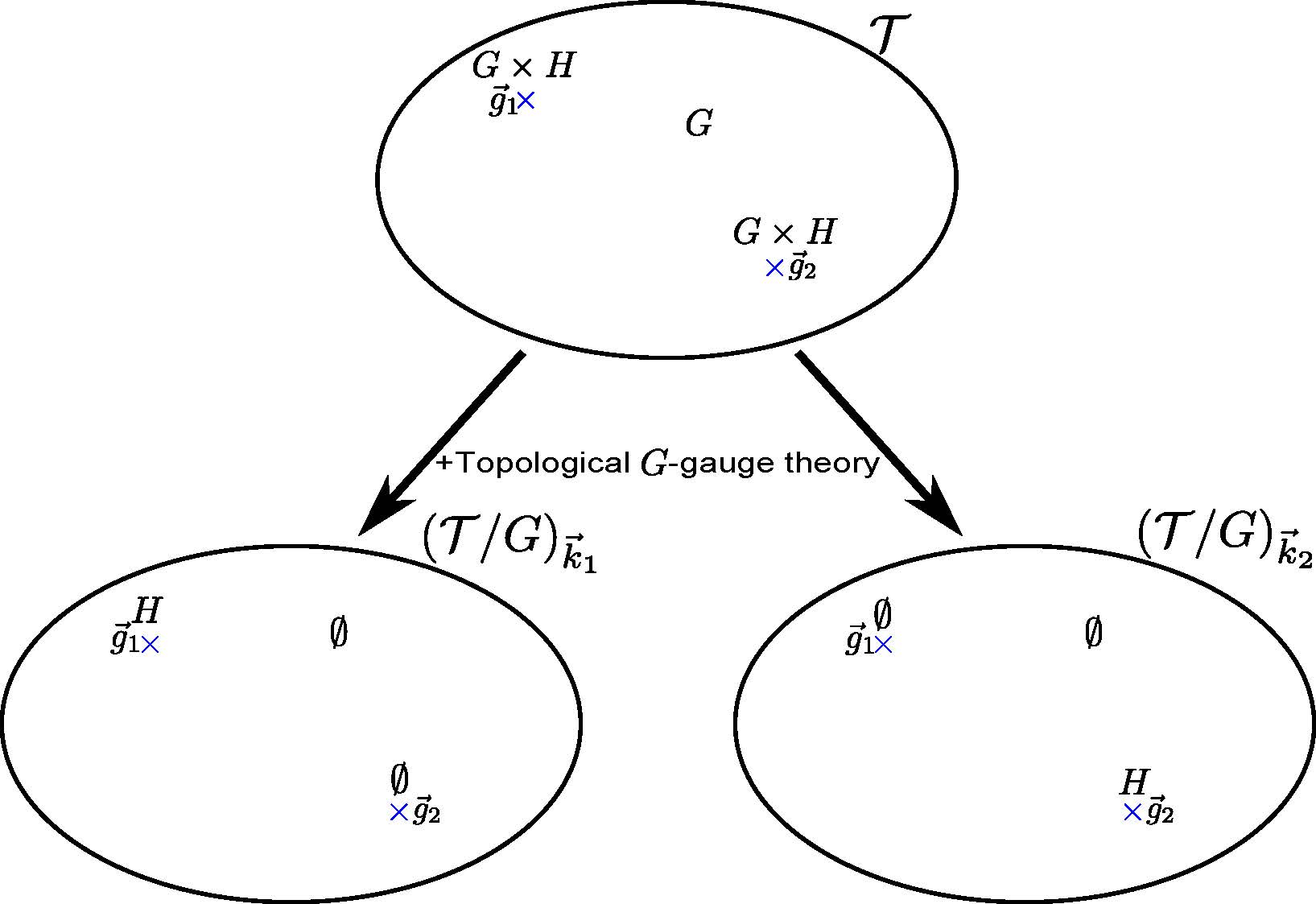
Understanding Global Inconsistency and ’t Hooft Anomaly Using Simple Quantum Mechanics
2025-2-21
This study explores the implications of global inconsistency and ’t Hooft anomalies for analyzing quantum field theories, using simple quantum mechanical models to provide valuable insights into these complex phenomena.
Theoretical Particle Physics