FieldsMathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
NEW
Do Superconductors Dream of Tsunamis? — A Cross-disciplinary Journey of Solitons2026-2-10
Tsunami-like solitons propagating over rocky-desert-like disordered backgrounds have been identified in a novel soliton equation derived from the theory of parity-mixed superconductivity.
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Superconductivity
-
Hybrid Quantum-Classical Computing for Quasiparticle Band Structures2025-12-12
The proposed hybrid quantum-classical computing method enables practical calculations of quasiparticle band structures to expand the possibilities for quantum materials research.
Electron states in condensed matter
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
Hanbury–Brown Twiss Effect Demystified—Free-space Ultrasound Steals the Show—2025-7-14
”Second-order fringes” rings a bell? ”Which-path” echoes a quantum sequel?
”Spoofing decoherence” sounds like a plan? All this is not about photons, actu-
ally. Fast forward, and let the answer reveal itself soon. Oops, too loud?Electromagnetism, optics, acoustics, heat transfer, and classical and fluid mechanics
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
Higher-Order Topological Phases in Magnetic Materials with Breathing Pyrochlore Structures2025-4-7
A simple example of a higher-order topological phase, in which the symmetry decreases step-by-step from the bulk to the corner, is realized in a magnetic system with a pyrochlore structure and is characterized by a series of quantized Berry phases defined for the bulk, surface, and edge.
Electronic structure and electrical properties of surfaces and nanostructures
Magnetic properties in condensed matter
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
PICKUP
Exploring the Vibrant Interplay of Machine Learning and Physics2025-3-13
This Journal of the Physical Society of Japan Special Topics edition explores how physics and machine learning complement each other and can solve unresolved problems in physics.
Cross-disciplinary physics and related areas of science and technology
Electron states in condensed matter
Elementary particles, fields, and strings
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Statistical physics and thermodynamics
Superconductivity
-
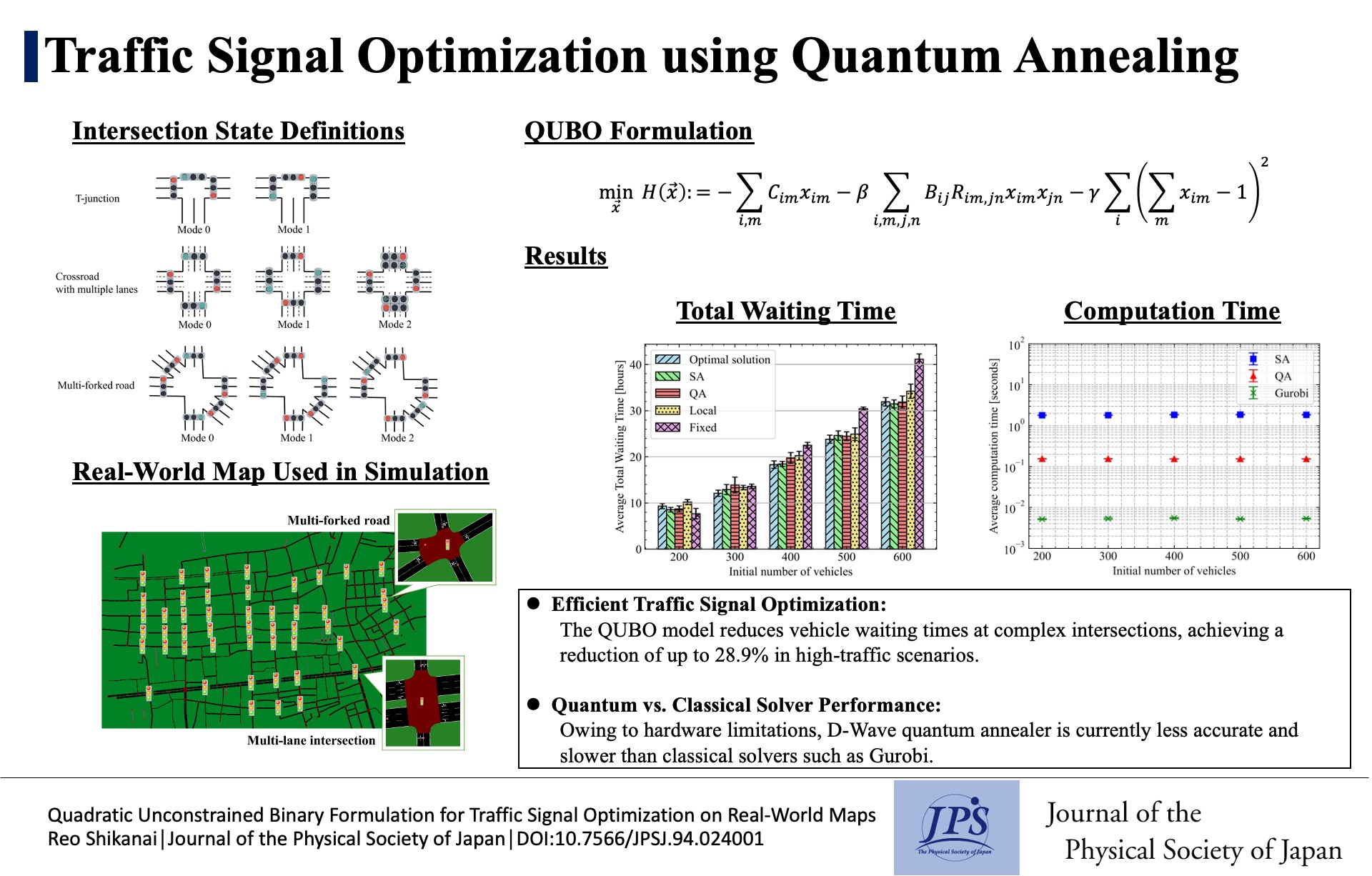Traffic Signal Optimization using Quantum Annealing2025-2-25
This paper introduces a QUBO model for traffic signal optimization on real-world maps. Using D-Wave quantum annealing and SUMO simulations, the model reduces vehicle waiting times, but underperforms classical solvers.
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
A Promising Solution to Nucleon–Nucleon Inverse Scattering Problem2024-10-7
This study deals with the inverse elastic two-body quantum scattering problem using Volterra approximations and neural networks, offering a novel approach for solving complex nonlinear systems.
General and Mathematical Physics
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Nuclear physics
-
PICKUP
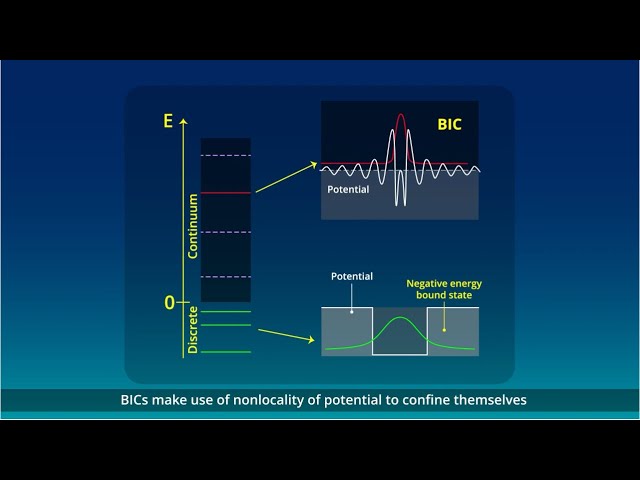A New Method for Finding Bound States in the Continuum2024-10-1
This study presents a general theory for constructing potentials supporting bound states in the continuum, offering a method for identifying such states in real quantum systems.General and Mathematical Physics
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Nuclear physics
-
PICKUP
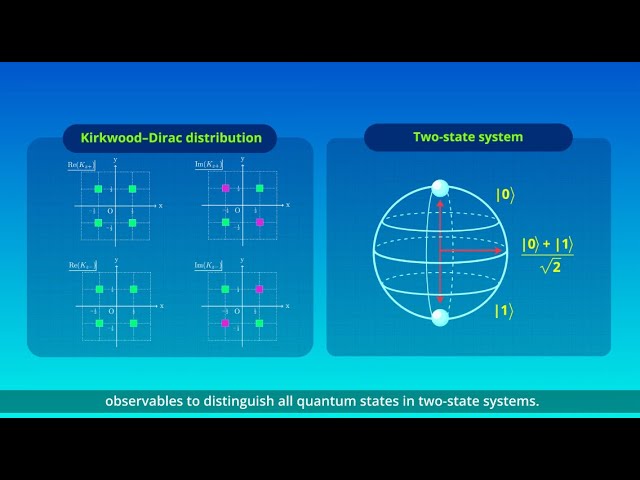General Quasi-Joint Probabilities on Finite-State Quantum Systems2024-8-15
This study investigates the properties of general quasi-joint probability distributions in finite-state quantum systems, revealing the Kirkwood-Dirac distribution as among the most favorable. This highlights the importance of complex distributions in understanding quantum probability.
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
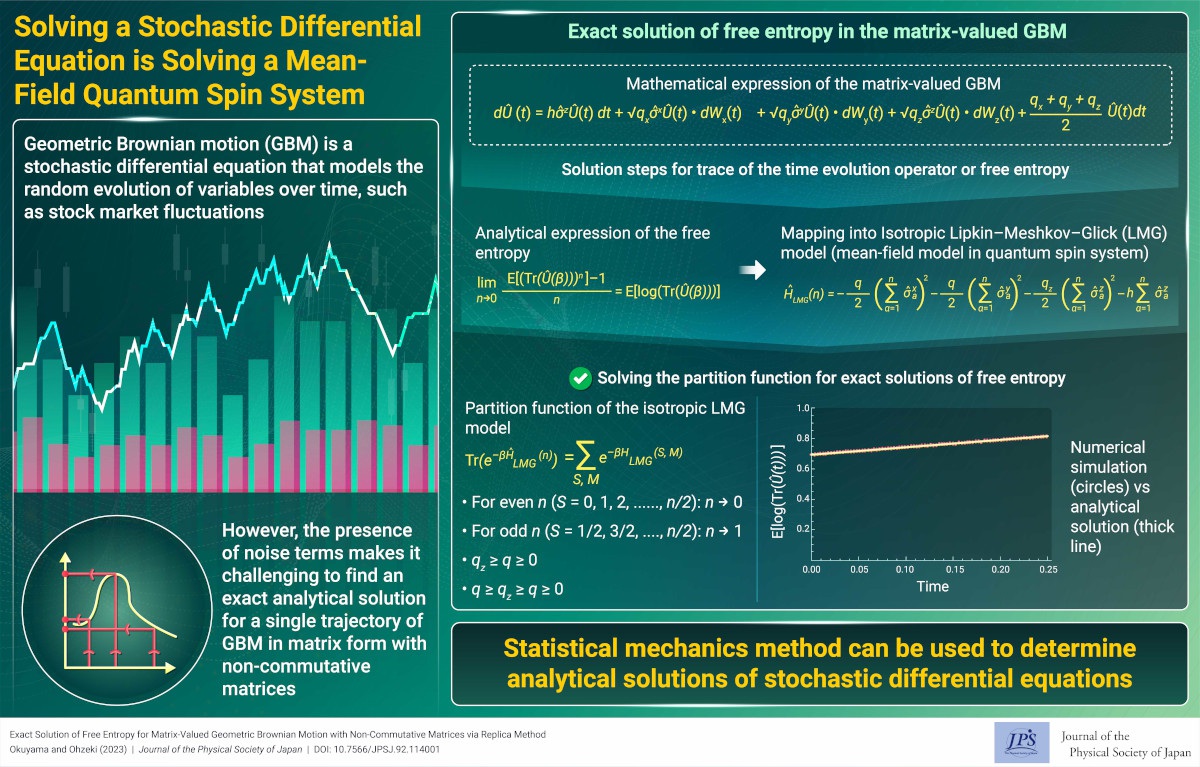Solving a Stochastic Differential Equation is Solving a Mean-Field Quantum Spin System2024-5-16
The replica method maps matrix-valued geometric Brownian motion to a mean-field quantum spin system. This correspondence makes it possible to obtain an exact solution for matrix-valued geometric Brownian motion.
Magnetic properties in condensed matter
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Statistical physics and thermodynamics
-
PICKUP
Quantum Mechanics of One-Dimensional Three-Body Contact Interactions2024-2-13
The quantum mechanical description of topologically nontrivial three-body contact interactions in one dimension is not well understood. This study explores the Hamiltonian description of these interactions using the path-integral formalism.
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Theoretical Particle Physics
-
PICKUP
Exploring Recent Advances in the Physics of Biofluid Locomotion2023-12-8
This Special Topics Edition of the JPSJ describes the latest advances in the field of biofluid locomotion, shedding light on the underlying physics behind the movement of organisms that swim and fly.
Cross-disciplinary physics and related areas of science and technology
Electromagnetism, optics, acoustics, heat transfer, and classical and fluid mechanics
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Measurement, instrumentation, and techniques
Statistical physics and thermodynamics
Structure and mechanical and thermal properties in condensed matter
-
Topological Properties of the Periodic Toda Lattice: Analogy with the Thouless Pump2023-8-8
We find that the periodic Toda lattice belongs to the same topological class as the Thouless pump.
Electronic structure and electrical properties of surfaces and nanostructures
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
PICKUP
Towards a New Phase in Materials Science with Hyperordered Structures2023-5-1
A Special Topics edition of the Journal of the Physical Society of Japan features articles discussing recent advancements in hyperordered structures in materials, their applications, and the techniques for observing them.
Atomic and molecular physics
Cross-disciplinary physics and related areas of science and technology
Dielectric, optical, and other properties in condensed matter
Electron states in condensed matter
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Structure and mechanical and thermal properties in condensed matter
-
PICKUP
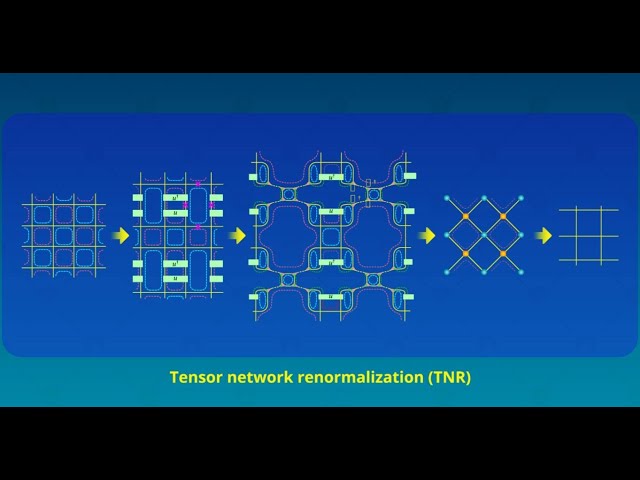Tensor Networks Across Physics2022-6-7
Researchers from Japan provide the first comprehensive review of the historical development of tensor networks from a statistical mechanics viewpoint, with a focus on its theoretical background.
Magnetic properties in condensed matter
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Statistical physics and thermodynamics
-
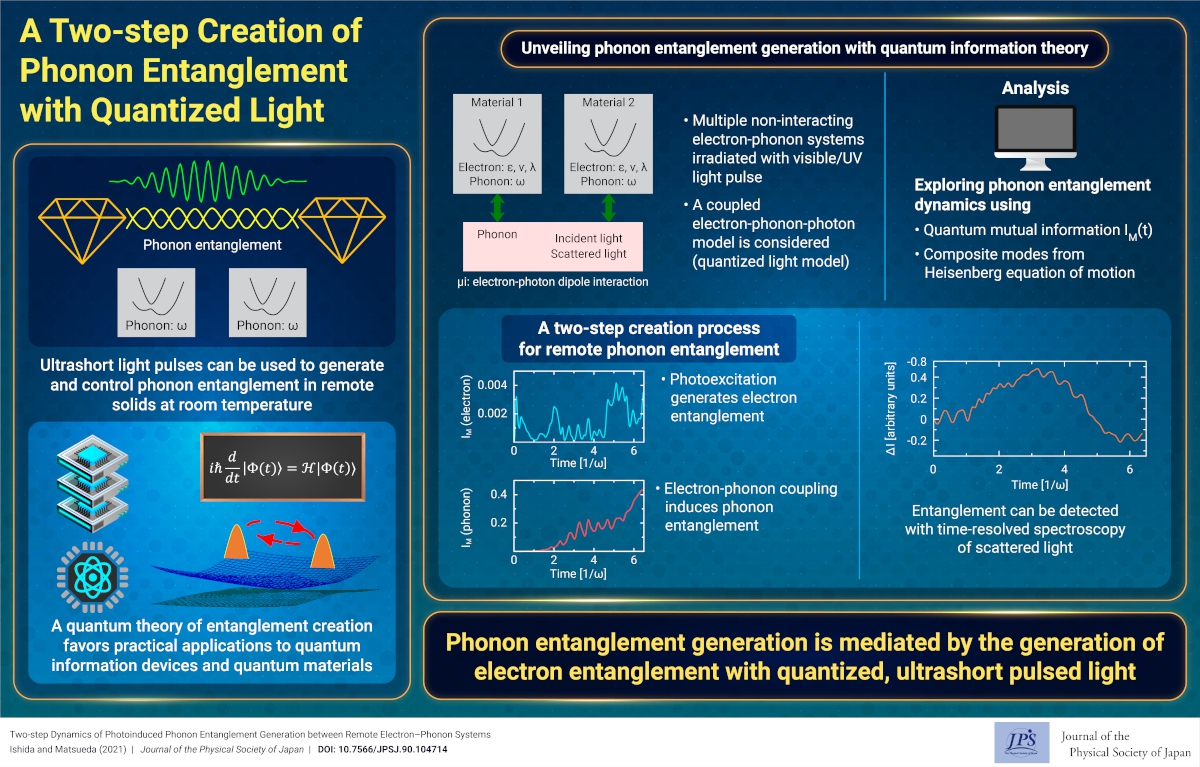
A Two-step Creation of Phonon Entanglement with Quantized Light
2021-12-28
Dynamics of photoinduced quantum entanglement generation between phonons is theoretically revealed. The results contribute to the study of fundamental theoretical problems within quantum dynamics of photoinduced phase transitions and quantum information science.
Dielectric, optical, and other properties in condensed matter
Electromagnetism, optics, acoustics, heat transfer, and classical and fluid mechanics
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
PICKUP
Generalizing Poisson Algebra with Geometry2021-9-6
Using a differential geometric interpretation of Hamiltonian mechanics, a generalized Poisson bracket formulation is developed for a three-dimensional phase space characterized by a triplet of canonical variables.
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
PTEP SPECIAL SECTION
Atoms Trapped with Light Behave Like a Dissipative Quantum System2021-7-19
A team of researchers from Japan experimentally realize, for the first time, a dissipative, parity-time symmetric, many-body quantum system from ultracold atoms trapped in an optical lattice.Gases, plasmas, electric discharges, accelerators, and beams
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
PTEP SPECIAL SECTION
A Quantum Description of Physical Systems with Non-real Energies2021-7-19
While quantum systems are traditionally described by Hermitian Hamiltonians, the formalism is extendable to a non-Hermitian description for systems that are dissipative or obey parity-time symmetry.Electron states in condensed matter
Gases, plasmas, electric discharges, accelerators, and beams
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Nuclear physics
-
PICKUP
Random Numbers Can Help Solve Difficult Problems in Many-body Physics2021-3-29
Theorists review a random state vector-based description of quantum many-body systems which helps greatly reduce the computational burden involved in their numerical simulations, opening doors to applications in quantum computing.
Electronic transport in condensed matter
Magnetic properties in condensed matter
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
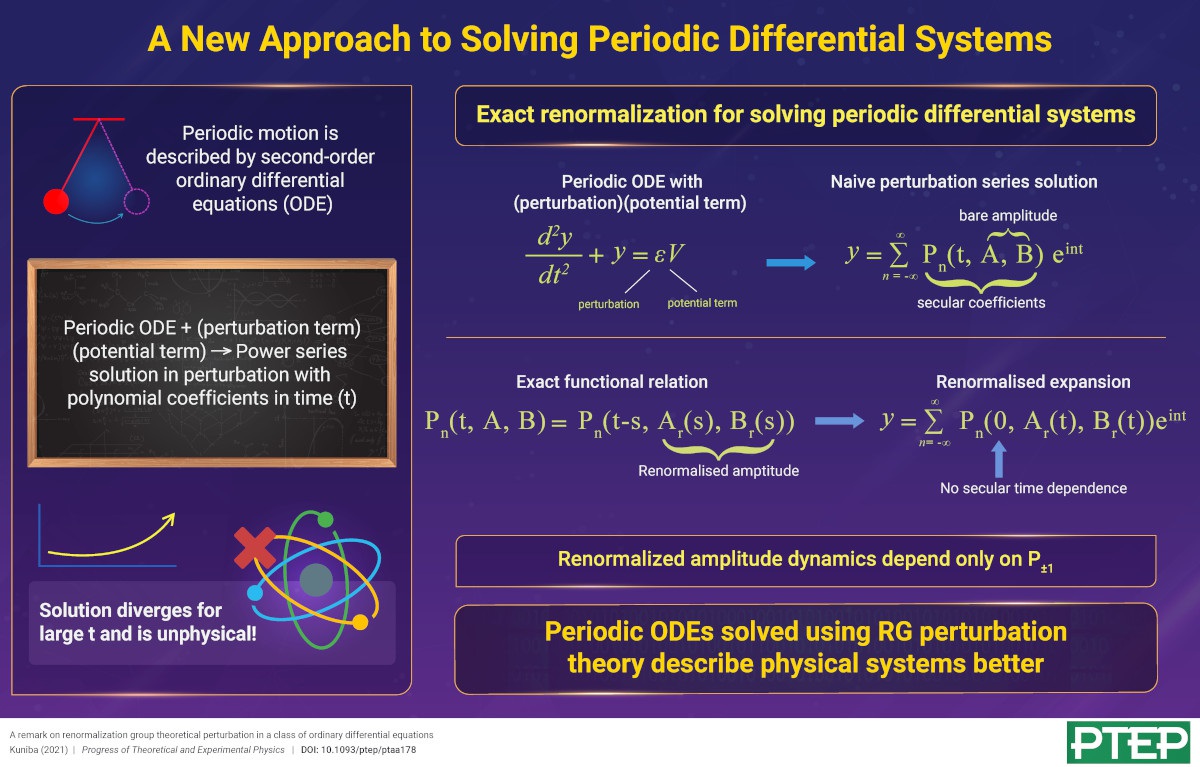A New Approach to Solving Periodic Differential Systems2021-3-29
Mathematicians and physicists are well acquainted with second-order ordinary differential equations (ODE), the most prominent of them being the class of equations that govern oscillatory motion.
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
PICKUP
Hybrid Quantum–Classical Algorithms: At the Verge of Useful Quantum Computing
2021-3-22
Scientists discuss the recent progress in algorithms that have enabled hybrid quantum–classical computers, which has brought the quest to realize useful quantum computing much closer to its finish line.
Cross-disciplinary physics and related areas of science and technology
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
-
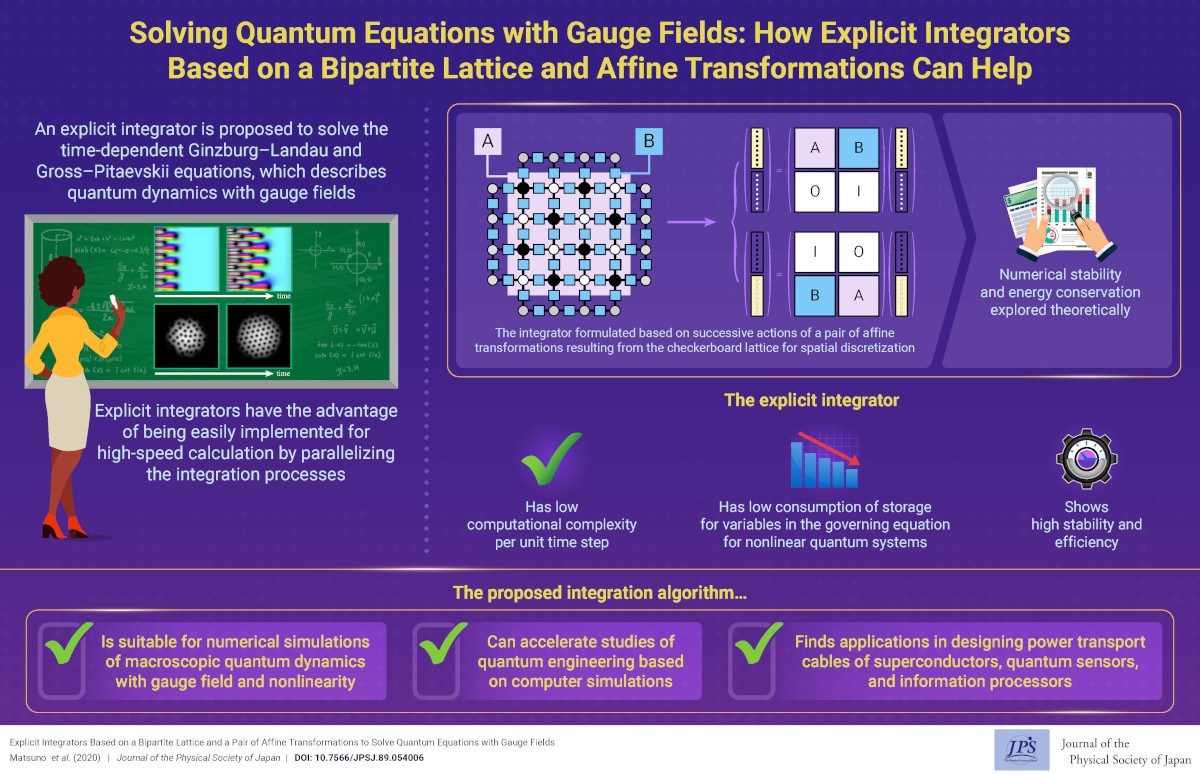
Solving Quantum Equations with Gauge Fields: How Explicit Integrators Based on a Bipartite Lattice and Affine Transformations Can Help
2021-3-15
We proposed an explicit numerical integrator consisting of affine transformation pairs resulting from the checkerboard lattice for spatial discretization. It can efficiently solve time evolution equations that describe dynamical quantum phenomena under gauge fields, e.g., generation, motion, interaction of quantum vortices in superconductors or superfluids.
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Superconductivity