View larger image

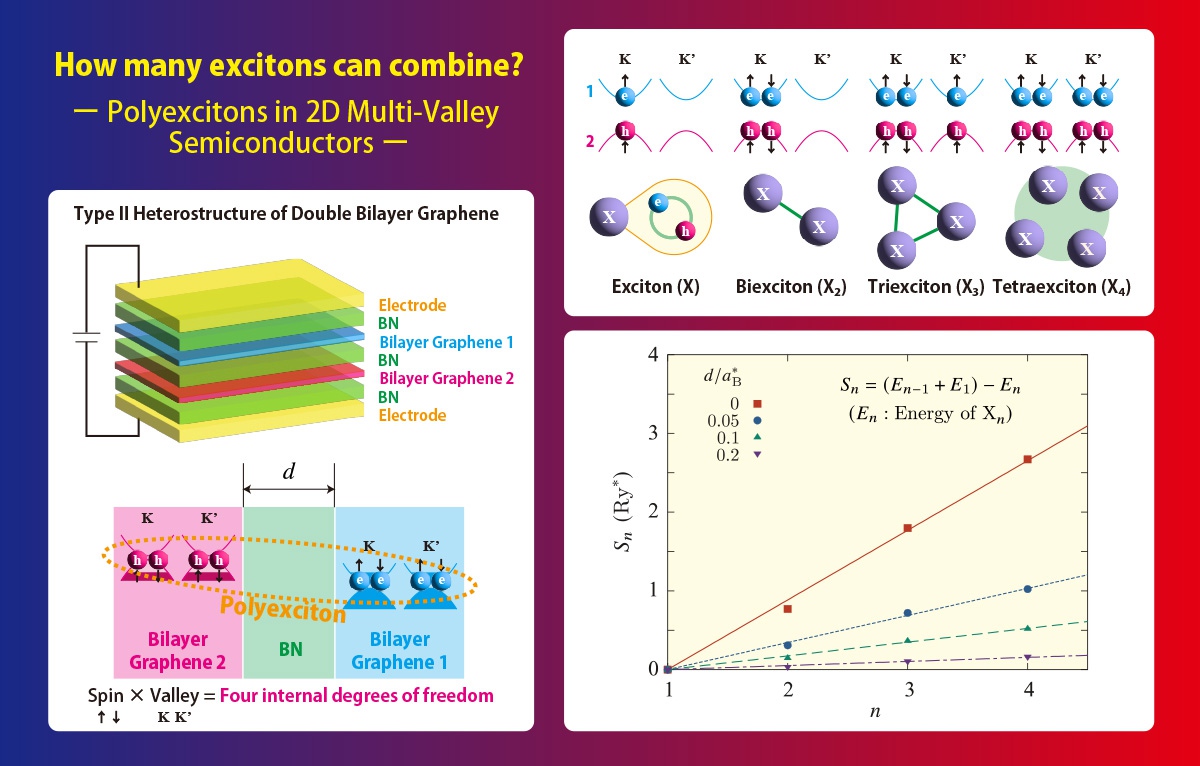
Polyexcitons are composites of multiple electron-hole pairs. In strongly photoexcited intrinsic semiconductors or type II semiconductor heterostructures, an electron in conduction bands and a hole in valence bands naturally form an exciton, and further, a pair of excitons coalesces into a biexciton. These composites have been studied in an analogy to hydrogen atoms or molecules. A common expectation is that excitons cannot form triexcitons, similar to hydrogen atoms that cannot form trimers. However, in multi-valley semiconductors, more than two excitons can be bound, because electrons and holes acquire the additional valley degrees of freedom that, combined with the spins, allow more than two electrons and holes to occupy the same position. This possibility was first identified by Wang and Kittel in 1972 and has been experimentally observed in pure bulk samples of silicon and diamond as the photoluminescence (PL) peaks almost equally spaced at energy intervals.

We consider the two-dimensional simplified model of the type II double-bilayer graphene heterostructures. The electrons and holes stay on different layers separated by a distance and interact with each other via Coulomb potentials. They also acquire four internal degrees of freedom because they have two spin and two valley degrees of freedom. This implies that our system can afford triexcitons and tetraexcitons, and that the quantum diffusion Monte Carlo simulation is free of the negative sign problem and can precisely evaluate the energies.

Notably, the separation energy required to pull out one exciton from the polyexciton grows almost exactly linearly with the exciton number. This behavior resembles the aforementioned PL peaks, indicating that the underlying physics is common between two and three dimensions. This further implies that all pairs of excitons inside the polyexciton are energetically bound by “chemical bonds” of equal strength, irrespective of the bound exciton numbers or the details of the system, for example, the interlayer distances.

(Written by K. Asano on behalf of all the authors)