View larger image

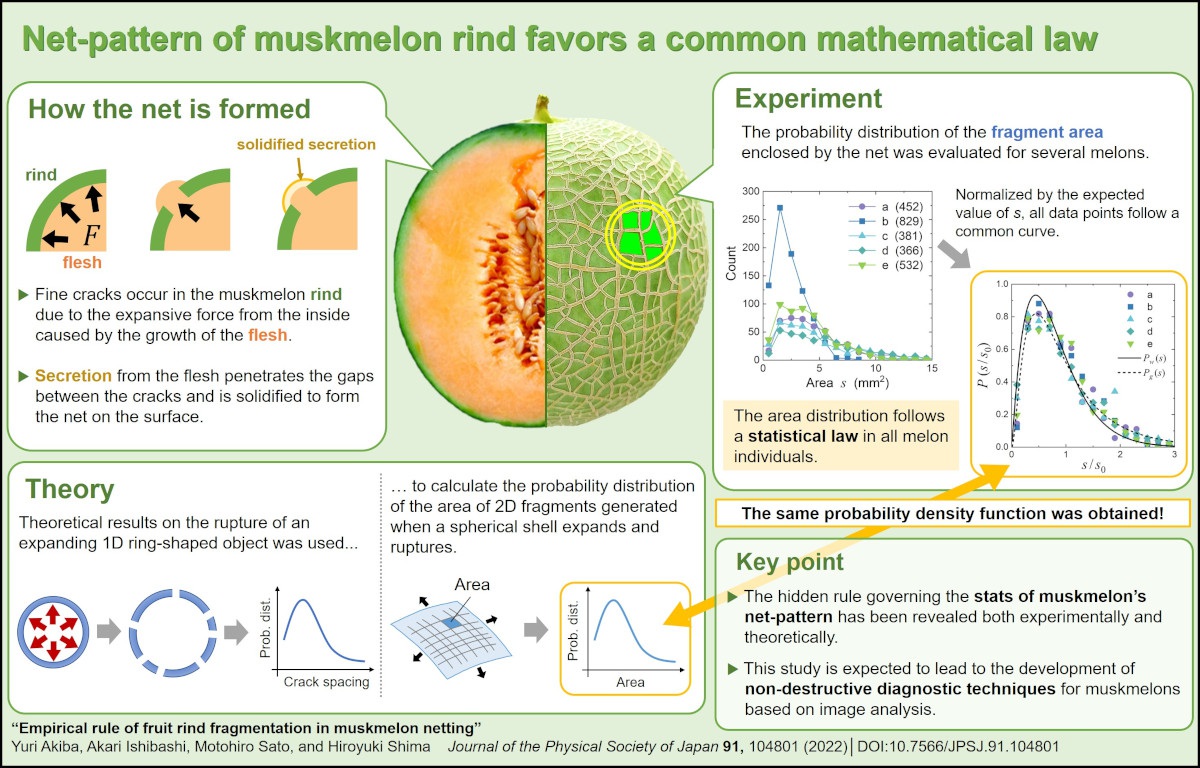
Professor Hiroyuki Shima’s research group at the University of Yamanashi, Japan, has discovered that the net-patterns observed on muskmelon (Cucumis melo) rinds follow a common statistical law deduced from fracture mechanics theory.

Empirically, there is a certain correlation between the net-pattern and the quality of netted melon species, like muskmelons. Yet, the geometric character of the melon’s net-pattern remains uninvestigated.

How do the melon nets form in the first place? Simply put, they are a “scab” that closes the wound on the melon’s epidermis. When the flesh of a muskmelon swells during the growth process, fine cracks appear across its surface. Subsequently, a wax-like substance (suberin, the main component of cork) is exuded from within the melon into the gaps between the cracks, filling them and then solidifying to form the muskmelon net-pattern. Similar cracking patterns are ubiquitous in nature, and are observed in dried paddy mud and aged concrete, where similar fracture processes are triggered by dehydration-induced shrinkage. This fact poses a question: are there any common scientific laws lurking in the cracking patterns of these different systems?

Shima’s research group analyzed the intricacy of the net-pattern of several commercially available muskmelons. They further derived the probability distribution curve of the area of ​​polygonal rind fragments surrounded by a mesh, and found an almost identical distribution curve in all individual melons. Furthermore, they found that this common distribution curve is not just a coincidence, but can be described by a modified Bessel function (a special mathematical function) derived from the fracture mechanics theory of spherical shell structures. Specifically, the experimentally-derived law concerning the melon’s net-pattern has been proved to be a scientific law backed by fracture mechanics theory.

In practice, the quality of muskmelons is mainly evaluated by their appearance, with the price difference due to grade differences being much larger than that of other fruits. Currently, this sorting work is performed visually by experts, such as producers and market participants. However, relying on such expertise can lead to arbitrary subjectivity in determining muskmelon grades. If the relationship between the fruit growth process and the accompanying net formation can be clarified, it would be possible to obtain an index that enables automatic and objective determination of the ripening degree of the fruit by visual inspection. Such an index can be applied to the cultivation management of muskmelons by improving cultivation practices.

(Written by H. Shima on behalf of all the authors.)