View larger image

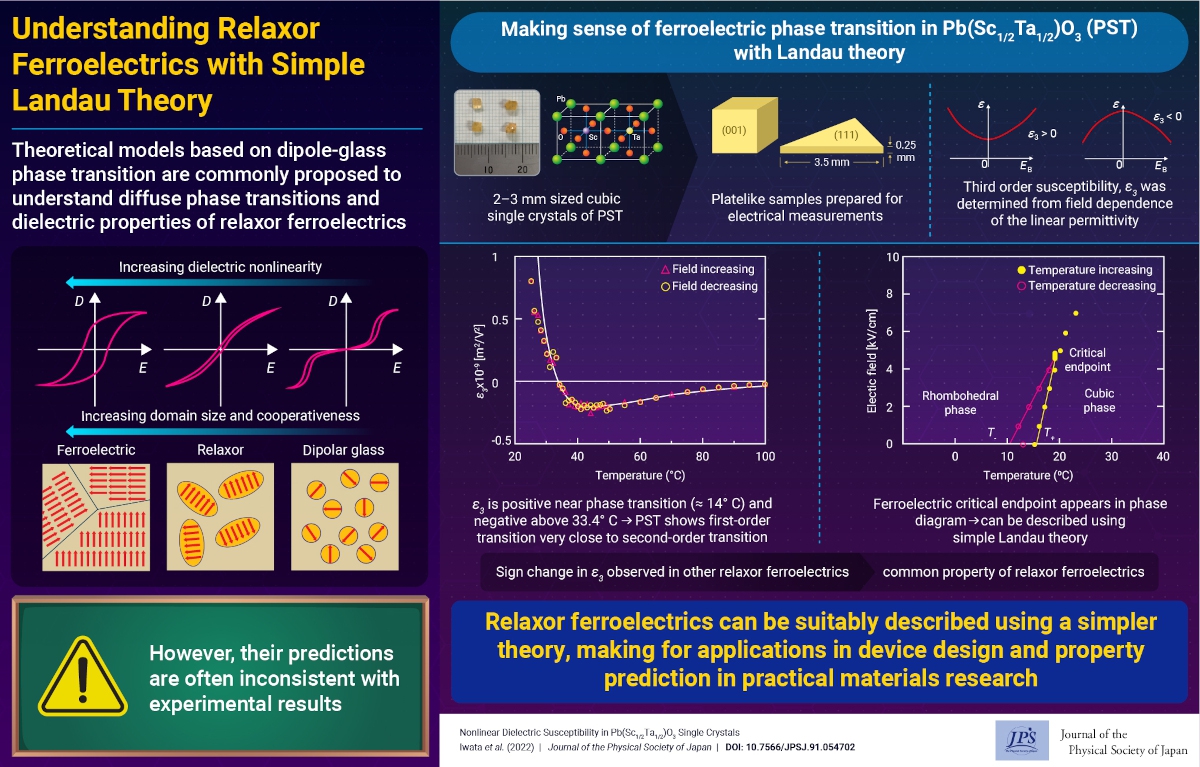
Pb(Sc_1/2Ta_1/2)O₃(PST) is a perovskite-type ferroelectric oxide that exhibits relaxor-like characteristics. A relaxor is a material that exhibits a diffuse phase transition with a wideband dispersion in dielectric permittivity over many orders of magnitude. One of the most challenging issues in the physics of ferroelectrics is to understand the inherent dielectric properties of relaxor ferroelectrics.

To explain the physical properties of relaxors, many theoretical models based on the dipolar-glass transition have been proposed wherein the third-order nonlinear dielectric susceptibility e₃ was theoretically predicted to indicate a negative divergence at the dipolar-glass transition temperature. However, it has been reported that in some relaxor ferroelectrics, the measured e₃ takes positive values without any indication of divergence near the temperature T_m at which the linear permittivity is maximum. This is inconsistent with the predictions made by the theoretical models based on the dipolar-glass phase transition. Therefore, to explain the temperature dependence of e₃, a new model is required. The ferroelectric critical endpoint (CEP) in the temperature–field phase diagram in many perovskite relaxor ferroelectrics has been extensively investigated. The PST temperature–field phase diagram has been obtained, and the existence of ferroelectric CEP was demonstrated. The appearance of the ferroelectric CEP in relaxors implies that relaxor ferroelectrics can be investigated based on the simple Landau-type free-energy density, similar to a conventional ferroelectric material, without any complex models based on dipolar-glass phases. Under these circumstances, in the present study, the linear and nonlinear dielectric susceptibilities in the paraelectric phase of PST were measured. The results were explained based on the Landau-type free-energy density.

The experimental results reveal that e₃ takes a positive value near T_m (approximately 14 °C) and becomes negative above T₁ = 33.4 °C. It was concluded that the positive e₃ near T_m in PST results from the first-order transition because the sign of b (coefficient of the fourth-order term of the polarization in the Landau-type free-energy density) directly depends on the sign of e₃. Furthermore, a change in the sign of e₃ near the transition temperature in PST indicates that b is relatively small, thereby implying that the phase transition in PST is close to the second-order transition. Such a change in the sign of e₃ in paraelectric phase has been reported for several perovskite-type ferroelectrics, such as BaTi_1–xZr_xO₃, PZN–PT, and PMN–PT, which indicates that it might be a property common to many perovskite ferroelectrics.

In this study, the relationship between the third-order susceptibility e₃ and ferroelectric phase transition in PST was clarified based on macroscopic thermodynamics.

(written by M. Iwata on behalf of all authors)