How Good is the Transition-State Theory?
© The Physical Society of Japan
This article is on
J. Phys. Soc. Jpn.
90,
114005
(2021)
.
For the first time, the main assumption of the transition-state theory for the decay of complex quantum systems across a potential barrier was realized using a microscopic many-body Hamiltonian.
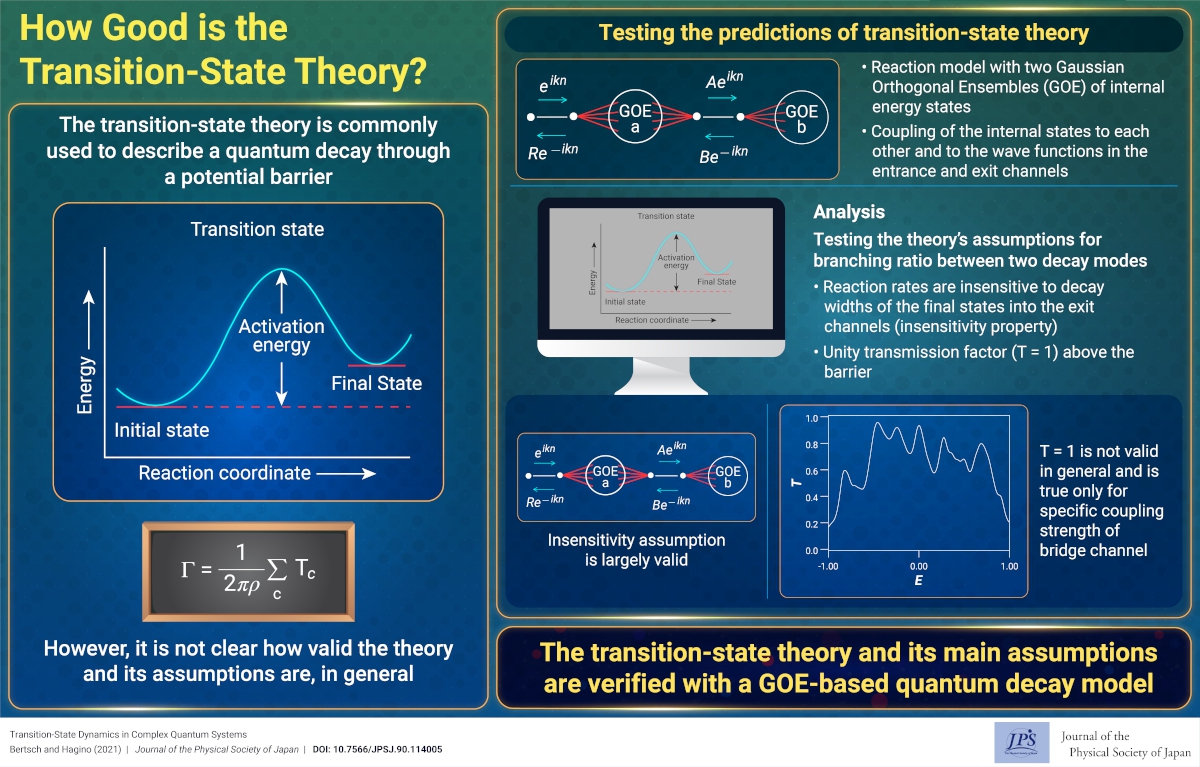
The decay of quantum systems through a potential barrier is ubiquitous in many fields of physics and chemistry, occurring in electron conduction within devices and quantum dots as well as chemical reactions, and nuclear fission. The usual framework for describing the barrier crossing is the "transition-state" theory, which was invented long ago to investigate chemical reactions and nuclear fission. The main assumption of this theory is that the decay rate is entirely determined at the highest point of the barrier and does not depend on what occurs afterward. This remarkable theory has been part of reaction theory since the 1930s and has been used in disciplines as widely distinct as chemistry and nuclear physics. However, this theory has not been validated for the quantum mechanics of many interacting particles.
In this study, a model was proposed to study reactions in systems with many interacting particles. The model allowed us to test whether the assumptions of the transition state theory could be satisfied in a full quantum theory. The model contains two reservoirs of internal states connected to each other by additional barrier-top states, and the reservoir states were considered using random matrix theory.
For the first time, we demonstrated that a main assumption of the transition-state theory can be easily satisfied by a more detailed theory, that is, the overall decay rate going through the far-side reservoir is largely determined by the barrier region and internal properties of the reservoirs, and is insensitive to the individual decay rates of the states out of the far-side reservoir.
In a subsequent paper (K. Hagino and G.F. Bertsch, Phys. Rev. E104, L052104(2021)), we applied the same model to discuss the variation of the decay rates between states. There is a well-established theory known as the Porter-Thomas distribution that has been validated for many systems, including atomic spectra, chemical reaction spectra, and nuclei. Surprisingly, our transition-state model revealed that this distribution differed depending on how large the individual rates were. The new distribution followed a different random matrix model, namely the Gaussian Unitary Ensemble, proposed by Dyson in 1960.
(Written by K. Hagino on behalf of all authors)
J. Phys. Soc. Jpn.
90,
114005
(2021)
.
Share this topic
Fields
Related Articles
-
Overcoming Phase Transitions for Faster Quantum Annealing
Statistical physics and thermodynamics
2025-3-27
This study presents an innovative method to address the problem of phase transitions in quantum annealing, resulting in an exponential speedup of the process.
-
Exploring the Vibrant Interplay of Machine Learning and Physics
Cross-disciplinary physics and related areas of science and technology
Electron states in condensed matter
Elementary particles, fields, and strings
Mathematical methods, classical and quantum physics, relativity, gravitation, numerical simulation, computational modeling
Statistical physics and thermodynamics
Superconductivity
2025-3-13
This Journal of the Physical Society of Japan Special Topics edition explores how physics and machine learning complement each other and can solve unresolved problems in physics.
-
Hyperuniform and Multifractal States in Bosonic Quasicrystalline Systems
Statistical physics and thermodynamics
Structure and mechanical and thermal properties in condensed matter
2025-2-10
Quantum states can be categorized as hyperuniform or multifractal based on electronic characteristics. This study demonstrates that bosonic quasicrystalline systems exhibit hyperuniform or multifractal quantum states.
-
Implementation of Nuclear Many-Body Wave Functions via Superpositions of Localized Gaussians
Nuclear physics
2025-1-9
An extended version of antisymmetrized molecular dynamics integrated with a mean-field model is proposed, and its potential is demonstrated.
-
Revival of JRR-3: A New Frontier in Neutron Scattering Research
Cross-disciplinary physics and related areas of science and technology
Elementary particles, fields, and strings
Magnetic properties in condensed matter
Measurement, instrumentation, and techniques
Nuclear physics
2024-11-12
This Special Topics edition of JPSJ details the capabilities and upgrades made to the instruments at JRR-3, since its shutdown after the Great East Japan Earthquake and 2011.




