View larger image

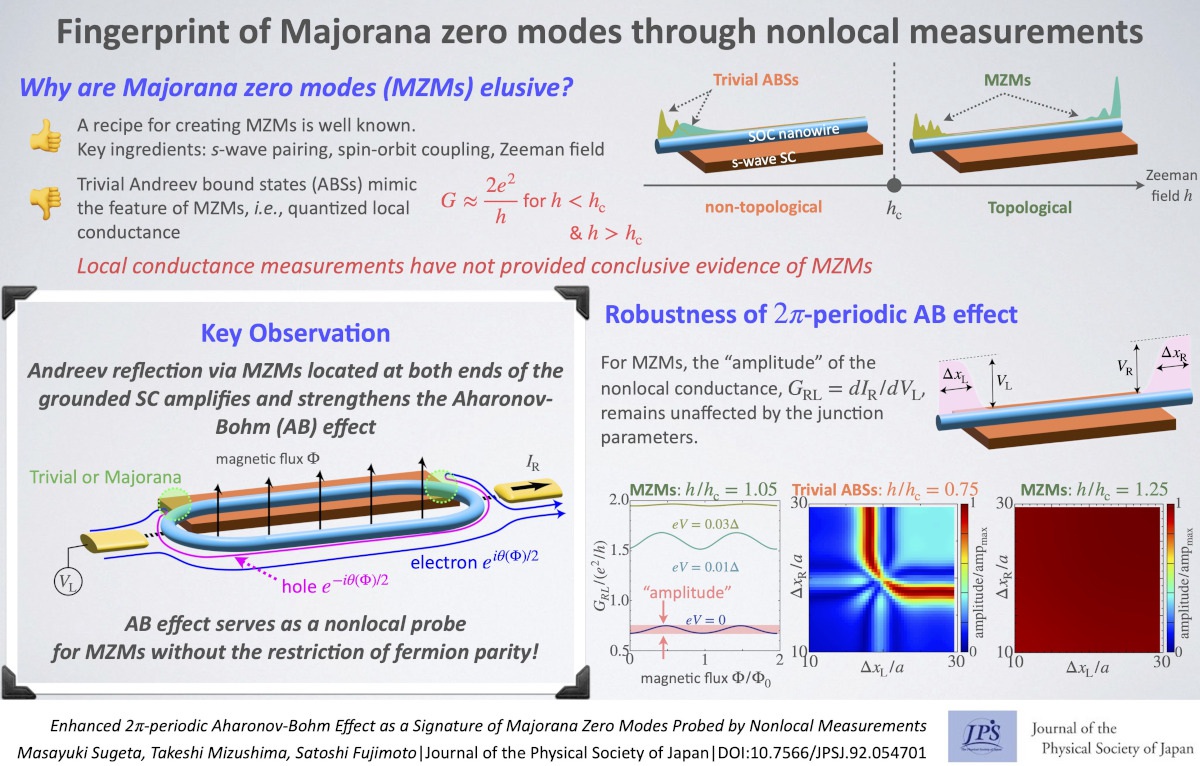
Electrons on the surface of topological superconductors behave as if they are split into two separate locations, a phenomenon known as fractionalization. This feature distinguishes Majorana fermions, specifically Majorana zero modes (MZMs), which have been studied for potential application in topological quantum computations. However, conventional local measurements, such as the quantization of local conductance, have failed to detect them because such characteristics are smeared by the trivial Andreev-bound states arising from inhomogeneous potentials around junctions. The nonlocality of MZMs, which arises from fractionalization, necessitates a new detection method. The two bound states at both ends of a one-dimensional topological superconductor retain nonlocal correlations, indicating their origin from a single electron. As this remarkable property is absent in trivial bound states, its detection would provide conclusive evidence of MZMs. However, this requires a floating superconductor that preserves the parity of electrons, which hinders experimental realization.

We highlight the significance of the nonlocality of MZMs (electron fractionalization) in considerably amplifying and strengthening the Aharonov-Bohm (AB) effect, even in grounded superconductors where the parity of electrons is not conserved.

We examined a loop-shaped junction system consisting of a one-dimensional topological superconductor and metal lead wire, and proposed nonlocal conductance measurements to observe the AB effect caused by a magnetic flux penetrating the loop. In general, Andreev reflection occurs at the interface between a superconductor and metal. When electrons in a metal undergo Andreev reflection repeatedly at both ends of the superconducting wire, the nonlocal conductance oscillates with 2π periodicity as a function of the magnetic flux Φ. Multiple Andreev reflections occur at two different junctions when the bound state energies at the two interfaces are close to each other. However, in the topological phase, the energies of the MZMs at both interfaces match closely. This reflects the aforementioned fractionalization phenomenon, leading to a robust AB effect. Our calculations indicated that in the non-topological phase, the AB effect through trivial bound states was considerably influenced by the parameters of the inhomogeneous potentials at the two interfaces and only occurred in a very narrow range of parameters. However, in the topological phase, the AB effect caused by MZMs was robust in all parameter regions. Unlike other nonlocal correlations such as Majorana-mediated teleportation, this phenomenon usually occurs without the restriction of fermion parity. The stability of the AB effect against interface details is crucial for detecting MZMs. MZMs and trivial bound states are more distinguishable in nonlocal correlation measurements than in local conductance measurements. Our study proposes that nonlocal correlation measurements may lead to new developments in the quest for MZMs in topological superconductors.

(written by T .Mizushima on behalf of all authors.)