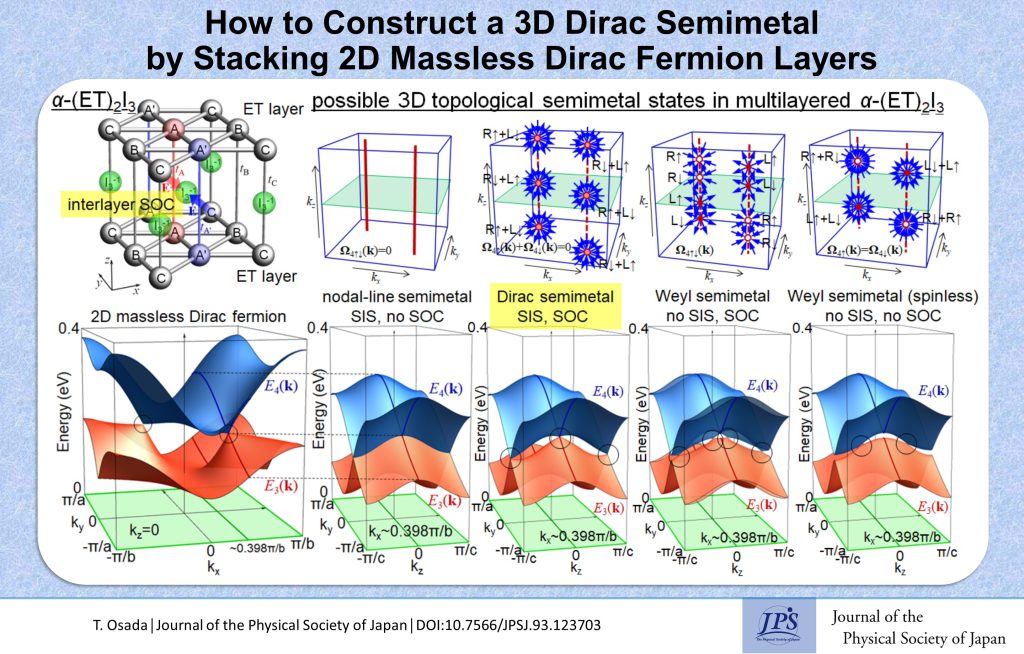
Dirac and Weyl semimetals are three-dimensional (3D) topological semimetals in which the conduction and valence bands touch at nodal points with a linear dispersion in the 3D Brillouin zone (BZ). They exhibit characteristic magnetotransport phenomena, negative longitudinal magnetoresistance and a planar Hall effect, resulting from the chiral anomaly. Recently, a layered organic conductor, α-(ET)₂I₃, exhibited these phenomena at low temperatures, indicating that it is a 3D Dirac or Weyl semimetal. However, it is well established that each ET layer of α-(ET)₂I₃ is a two-dimensional (2D) massless Dirac fermion system, where the conduction and valence bands touch at two nodes in the 2D BZ. Therefore, the question is whether and how 3D Dirac or Weyl semimetals can be formed by stacking 2D massless Dirac fermion layers.

Because the α-(ET)₂I₃ crystal has space inversion symmetry (SIS) and time reversal symmetry (TRS), the stacking must preserve these symmetries. Under SIS and TRS, the Weyl semimetal is never allowed, but the Dirac semimetal can be allowed because the total Berry curvature of the spin-degenerate bands is cancelled out. However, when simple interlayer hopping is introduced into the electronic structure model without breaking the SIS and TRS, the system usually becomes a 3D nodal-line semimetal, where 2D nodal points form nodal lines along the stacking direction in the 3D BZ. To realize a Dirac semimetal, we must consider spin–orbit coupling (SOC) in interlayer hopping. In the α-(ET)₂I₃ crystal, the ET conduction layer and the I₃⁻ anion layer are alternately stacked. Electrons hopping from one ET layer to the neighboring ET layer must penetrate the I₃⁻ layer, and the I₃⁻ configuration is unsymmetrical around some hopping paths. In fact, the I₃⁻ ion is located on one side of the interlayer hopping path between the A (or A’) sites of the neighboring layers and imposes a strong potential gradient on the hopping electrons, resulting in SOC. Note that SOC is relatively strong in interlayer hopping; however, it is generally considered weak in the ET layers because the ET molecule consists of light atoms. This interlayer SOC reflecting the I₃⁻ configuration opens a gap along the nodal line in the interlayer k_z-dispersion, leaving two Dirac points at k_z = 0 and π/c. Therefore, the interlayer SOC arising from the anion potential can realize the Dirac semimetal state while maintaining the SIS and TRS. If the SIS is broken by the introduction of interlayer hopping, each band exhibits zero-field spin splitting, and the Weyl semimetal state, where spin degeneracy is lifted, arises instead of the Dirac semimetal state.

(Written by Toshihito Osada on behalf of the authors)

Share this topic

Fields

Related Articles