Topological Aspects of a Nonlinear System: The Dimerized Toda Lattice

2022-3-16

JPS Hot Topics 2, 010

https://doi.org/10.7566/JPSHT.2.010

This article is on

Topological Edge States and Bulk-edge Correspondence in Dimerized Toda Lattice
(JPSJ Editors' Choice)

Motohiko Ezawa
J. Phys. Soc. Jpn. 91, 024703 (2022) .

A nonlinear topological phase is shown to emerge in the dimerized Toda lattice. It is experimentally detectable by measuring the voltage propagation in electric circuits.

View larger image

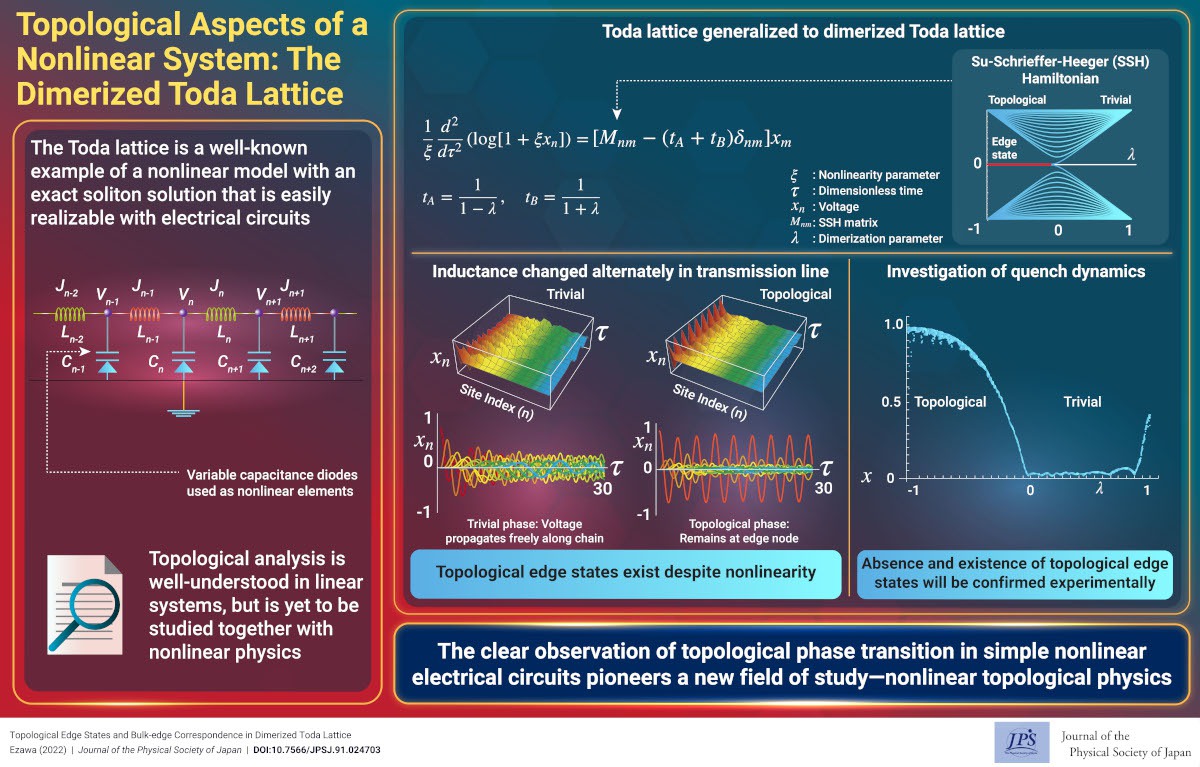
Nonlinear physics is an extensively studied field that is highlighted by the emergence of solitons and chaos. A soliton is a solitary wave that is stabilized by the nonlinear term. It is originally proposed in the surface wave of water and then found in various systems. The Toda lattice is a typical nonlinear model possessing an exact soliton solution. It is experimentally realized in a transmission line consisting of inductors and variable-capacitance diodes, where the variable-capacitance diodes provide the nonlinear elements. A stable voltage propagation was observed in this transmission line. In contrast, the topological physics is an emerging field, where characteristic topological edge states emerge in the topological phase. The Su–Schrieffer–Heeger (SSH) model is the simplest example of a topological insulator, where the bonds are alternating. To date, nonlinear and topological physics were studied independently. It is an interesting problem to study a nonlinear topological physics, which will open a new field of physics.

We generalize the Toda lattice to a dimerized Toda lattice as in the case of the SSH model. We show that this model is realized by changing the inductance alternately in the transmission line realizing the Toda lattice. This model has topological edge states although it is a nonlinear model. We verify it by investigating the quench dynamics, where we apply a voltage at the edge node and explore its time evolution. The voltage propagates freely along the chain in the trivial phase, whereas it remains at the edge node in the topological phase. Hence, the absence and the existence of the topological edge states are well signaled by the voltage propagation dynamics. Thus, nonlinear topological physics will be relatively easily realized and studied experimentally in electric circuits. This result will open a new field of nonlinear topological physics.

(Written by M. Ezawa)

Topological Edge States and Bulk-edge Correspondence in Dimerized Toda Lattice
(JPSJ Editors' Choice)

Motohiko Ezawa
J. Phys. Soc. Jpn. 91, 024703 (2022) .