Powered by Machine Learning: Obtaining Spectral Conductivity and Chemical Potential of Thermoelectric Materials from Experimental Data

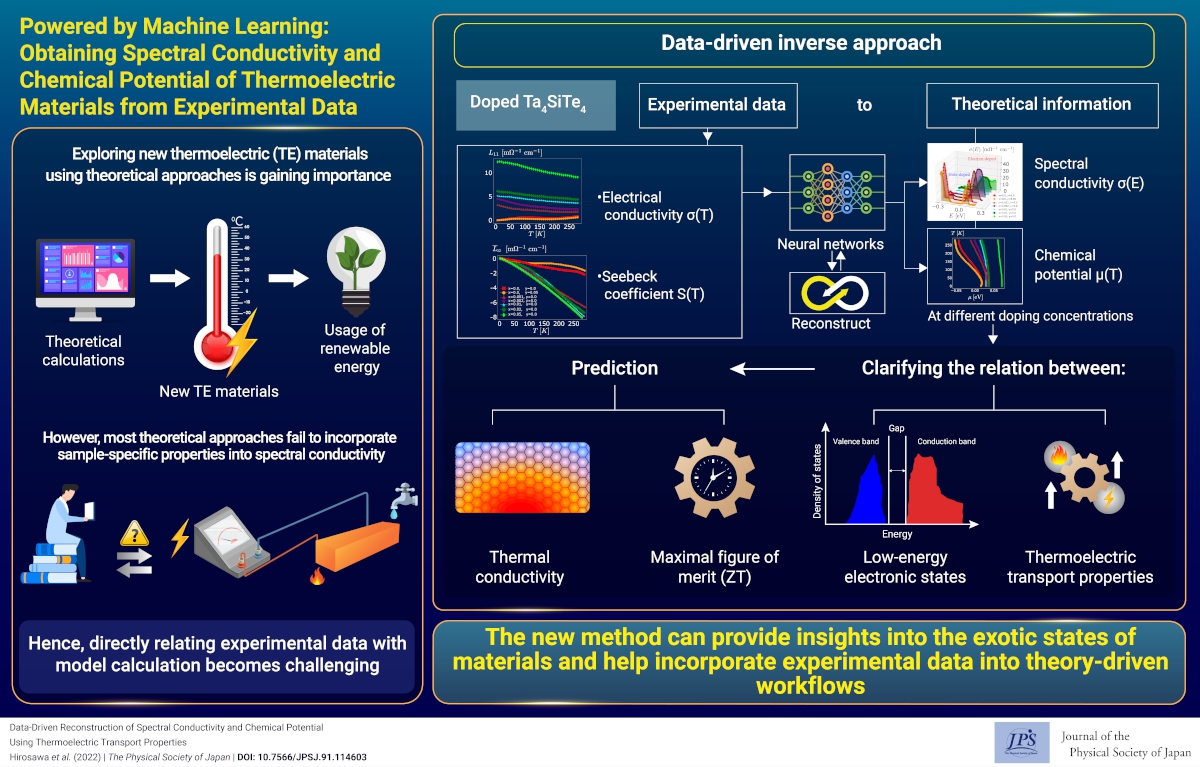
Thermoelectric materials offer an attractive path towards renewable energy by converting thermal energy into electric currents. The efficiency of thermoelectric materials is characterized by the dimensionless figure of merit $ZT$ , which cannot be easily increased because it requires that conflicting material properties be optimized.

Computational-based methods play a major role in accelerating the search for high-performance thermoelectric materials. When thermal currents are carried only by electrons, a simple expression called the Sommerfeld--Bethe (SB) relation relates the thermoelectric coefficients with the spectral conductivity, which is a function of the Fermi energy. This allows us to use a high-throughput approach in which the electrical conductivity $¥sigma(T)$ and Seebeck coefficient $S(T)$ are computed from the spectral conductivity using first-principles calculations. However, this approach is limited because the thermoelectric coefficients depend on sample-dependent properties such as material microstructures, chemical compositions, vacancies, charge impurities, and carrier concentrations. This means that a direct comparison of the experimental data with theoretical predictions is challenging.

In this study, we considered the inverse problem: can we reconstruct the spectral conductivity from the experimental data? The SB relation is a type of Fredholm integral equation and is known to be ill-conditioned for the inverse problem. Thus, we can estimate only an approximate solution. Our method employs a neural network to optimize the spectral conductivity and chemical potential that reproduce the experimental data of $¥sigma(T)$ and $S(T)$. Crucially, our data-driven inverse approach enables the sample dependence of the experimental data to be fully incorporated into the spectral conductivity.

We apply our method in analyzing experimental data of doped one-dimensional telluride Ta4SiTe4 [T. Inohara, et al., Appl. Phys. Lett. 110, 183901 (2017)]. Our model reproduces the experimental results and reveals the chemical doping dependence of the spectral conductivity and chemical potential. In addition, our method produces accurate estimates of the thermal conductivity of electrons and maximal figure of merit $ZT$ beyond the Wiedemann--Franz law, which is not valid in insulators and at high temperatures.

Reconstruction of the full energy dependence of the spectral conductivity, including the phenomenological relaxation time, opens a path for clarifying the underlying low-energy electronic states of high-performance complex thermoelectric materials. Because the spectral conductivity reflects both the bulk band structure and electron scattering, our method also gives insight into more exotic states such as strongly correlated electron systems with short-ranged interactions.

(written by T. Hirosawa on behalf of all the authors.)