Can a Node-Less Wave Function Have Higher Energy than Node-Full Ones?

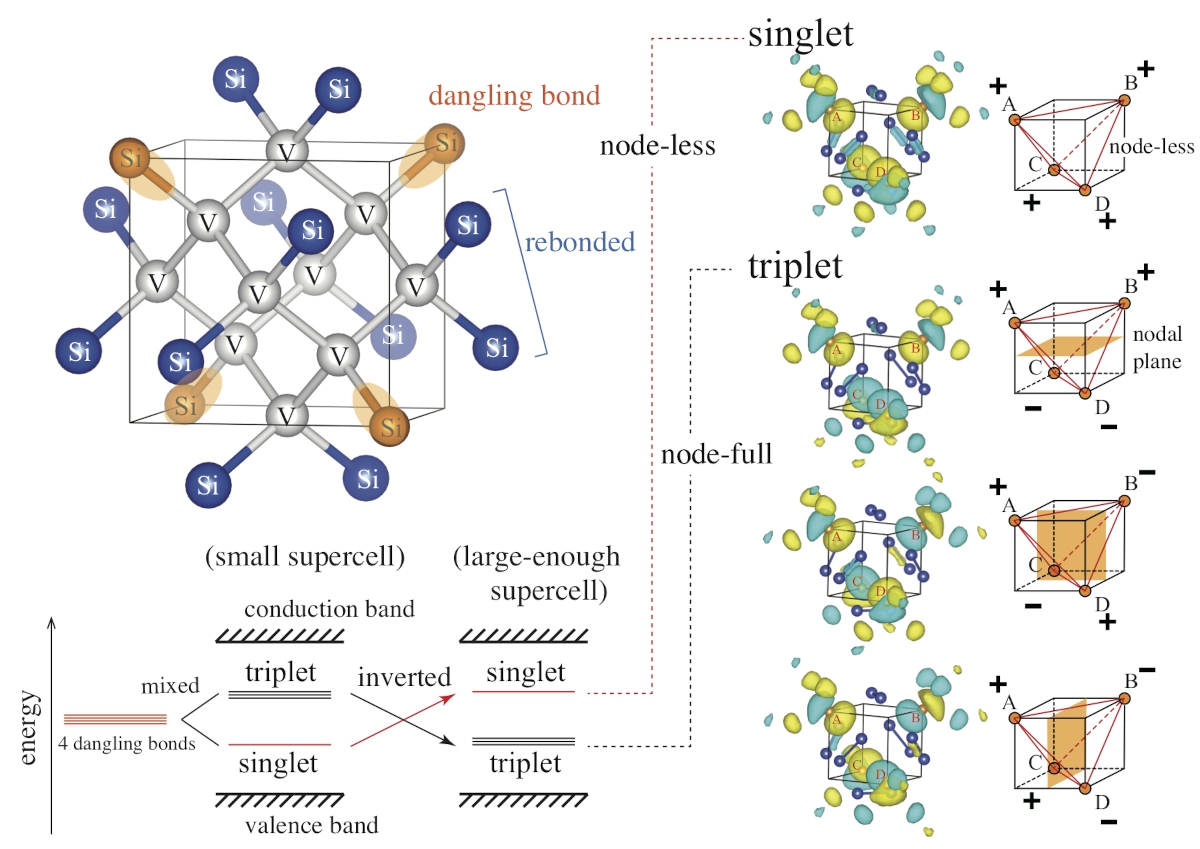
In quantum mechanics textbooks, a node-less wave function is described as having lower energy than that with nodal planes, because the kinetic energy increases with an increasing number of nodes. This statement has been thought to be universal.

However, we have recently found an exceptional case in the decavacancy of Si crystal, where node-less mixing of four dangling-bond orbitals (φ_A, φ_B, φ_C, and φ_D) in the singlet state leads to a higher energy than node-full mixing in the triplet states. That is,

where

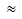Ψ_singlet (+φ_A+φ_B+φ_C+φ_D)/2,

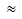Ψ_triplet (+φ_A+φ_B -φ_C -φ_D)/2,

                       (+φ_A -φ_B -φ_C +φ_D)/2,

                       (+φ_A-φ_B +φ_C -φ_D)/2.

This unexpected energy ordering is the enigma discussed and solved in our study.

Decavacancy V₁₀. is one of the magic number vacancies, obtained by removing a Si₁₀ cluster from an otherwise perfect Si crystal. Although the vacancy is accompanied by 16 dangling bonds, 12 of them are re-bonded with adjacent ones. Thus, we have only four dangling bonds remaining in V₁₀. The four dangling-bond orbitals (φ_A, φ_B, φ_C, and φ_D) are arranged under the T_d symmetry, which mix to generate the singlet and triplet electron states in the band gap, as described by Eq. (2). Our finding in Eq. (1) is surprising, because it seems to contradict a universal rule stated in the textbooks.

To clarify the underlying physics, we constructed a model to reproduce the energy ordering in Eq. (1), and successfully showed that such a non-intuitive electronic structure originates from the slight hybridization of the four dangling-bond states in the band gap with the 12 re-bond states outside the band gap. Here, the “re-bond states” refers to the six bonding states in the valence band and the six anti-bonding states in the conduction band, generated when 12 dangling bonds are paired with adjacent ones. Although such pairing makes the rebond states inactive, we found that the passivation was not perfect. They are slightly hybridized with the four dangling-bond states in the band gap, which make the energy of the node-less singlet higher than that of the node-full triplet.

We argue that this peculiar electronic structure is reflected in the Jahn-Teller instability of the system. We also note that large-scale DFT calculations are paramount for this work, because the supercell size must be large enough for the results of calculations to converge into Eq. (1).

(Written by K. Uchida on behalf of all authors.)