New Classification Theory for Topological Gapless Superconducting Nodes

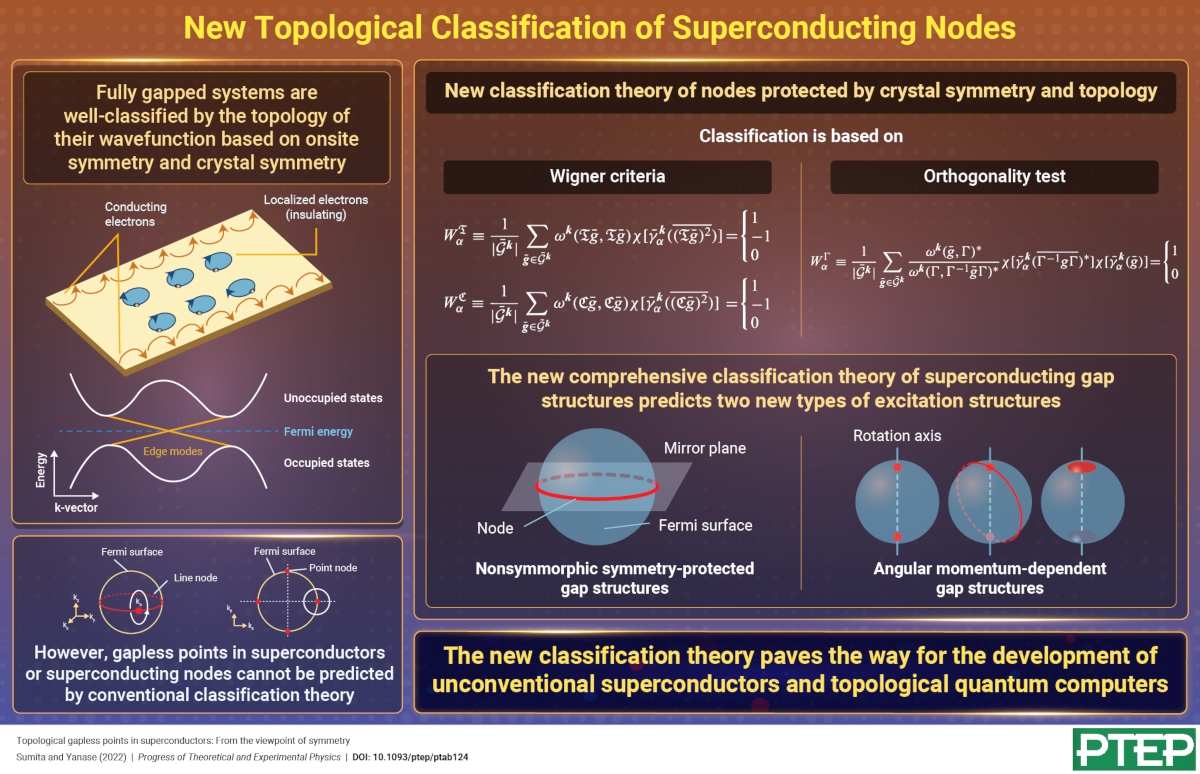
Topological phases of matter, such as topological insulators, semimetals, and superconductors, have garnered much attention in condensed matter physics. These are strange materials characterized by the presence of conduction states on the surface while the bulk remains insulating. Moreover, the surface states are protected by certain symmetries against physical deformations or defects.

It turns out that such systems can be classified by a “topological invariant” or a topological number such that two systems with the same topological number are equivalent. The topological invariant is classified by the symmetry and dimensionality of the system and is well-defined for gapped Hamiltonian systems. A well-known classification scheme is based on onsite symmetries, such as time-reversal symmetry, particle-hole symmetry, and chiral symmetry. However, recent schemes involve both crystal symmetry and onsite symmetry.

Interestingly, topological superconductors often have gapless points called “superconducting nodes” that are characterized by topological invariants, even though topology for the wavefunction can only be defined for gapped Hamiltonians. While there exist some classification theories for the superconducting order parameter predicting such nodes, they are sometimes incompatible with the actual superconducting gap structure and do not account for space group symmetry and higher-spin states.

In this paper, we present a new classification theory for superconducting nodes to resolve these two problems. We constructed this theory based on arguments from group theory and topology. An earlier topological classification theory focused on the d-dimensional Brillouin zone (BZ). However, since a band gap cannot exist in a whole d-dimensional BZ in nodal superconductors, we instead considered a p­-dimensional (p < d) sphere surrounding nodes in the BZ.

We fixed a specific k point in the BZ and then developed the classification theory on the high-symmetry points using the Wigner criteria and the orthogonality test. Our results predicted two new types of excitation structures, i.e., unconventional superconducting nodes protected by crystal symmetry and topology.

By performing classification on high-symmetry planes, we predicted nontrivial gap structures appearing from nonsymmorphic space group symmetry, which can be decomposed into a product of non-primitive lattice translation and a point group operation. Meanwhile, performing classification on high-symmetry lines helped predict nontrivial gap structures dependent on the angular momentum of the normal Bloch state.

Because these classification structures are determined only by symmetry, they can be universally applied to many candidate superconductors, potentially leading to the discovery of superconductors hosting unconventional nodes.